Temas
Para elevar una fracción a una potencia se aplica el exponente tanto el numerador como el denominador.

siempre que 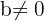
Ejemplo: Desarrolla la potencia 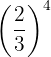


Potencias de fracciones con exponente negativo
Una potencia de una fracción con exponente negativo es igual a otra potencia cuya base es la inversa de la fracción original y con exponente positivo
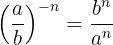
Ejemplo: Desarrolla la potencia 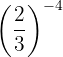
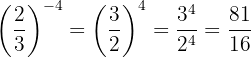
Propiedades de las potencias de fracciones
1Toda fracción elevada a la potencia cero es igual a uno.
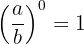
2Toda fracción elevada a la potencia uno es igual a la misma fracción.
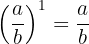
3El producto de potencias con la misma base es otra potencia con la misma base y su exponente es igual a la suma de los exponentes.

4La división de potencias con la misma base es otra potencia con la misma base y su exponente es igual a la diferencia de los exponentes.
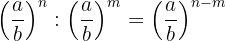
5La potencia de una potencia es otra potencia con la misma base y su exponente es igual al producto de los exponentes.

6El producto de potencias con el mismo exponente es otra potencia con el mismo exponente y su base es igual al producto de las bases.
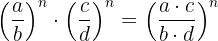
7El cociente de potencias con el mismo exponente es otra potencia con el mismo exponente y su base es igual al cociente de las bases.

Ejercicios propuestos
Simplifica las siguientes operaciones con potencias:
1
Las potencias tienen la misma base, entonces por la propiedad 3 la base es la misma y se suman los exponentes
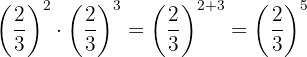
2
Las potencias tienen la misma base, entonces por la propiedad 3 la base es la misma y se suman los exponentes

Por la propiedad 2 toda fracción elevada a la potencia uno, es igual a la misma fracción

3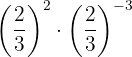
Las potencias tienen la misma base, entonces por la propiedad 3 la base es la misma y se suman los exponentes
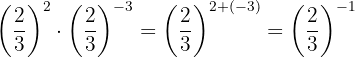
Para quitar el signo negativo del exponente, tenemos que escribir la fracción inversa y luego aplicamos la propiedad 2 que nos dice que toda fracción elevada a la potencia uno, es igual a la misma fracción
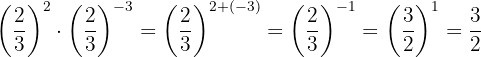
4
Las potencias tienen la misma base, entonces por la propiedad 3 la base es la misma y se suman los exponentes
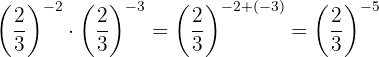
Para quitar el signo negativo del exponente, tenemos que escribir la fracción inversa
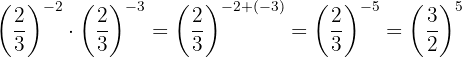
5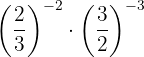
Como las potencias no tienen la misma base, tomamos la fracción inversa de la segunda potencia para obtener un exponente positivo

Por la propiedad 2 toda fracción elevada a la potencia uno, es igual a la misma fracción
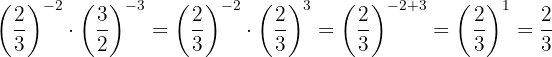
6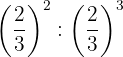
Las potencias tienen la misma base, entonces por la propiedad 4 la base es la misma y se restan los exponentes
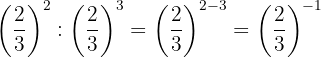
Para quitar el signo negativo del exponente, tenemos que escribir la fracción inversa; luego por la propiedad 2 toda fracción elevada a la potencia uno, es igual a la misma fracción
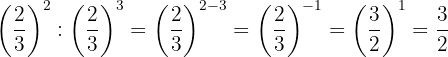
7
Las potencias tienen la misma base, entonces por la propiedad 4 la base es la misma y se restan los exponentes
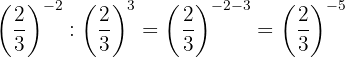
Para quitar el signo negativo del exponente, tenemos que escribir la fracción inversa
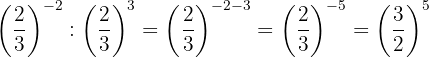
8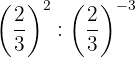
Las potencias tienen la misma base, entonces por la propiedad 4 la base es la misma y se restan los exponentes
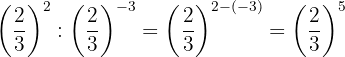
9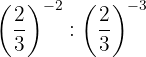
Las potencias tienen la misma base, entonces por la propiedad 4 la base es la misma y se restan los exponentes
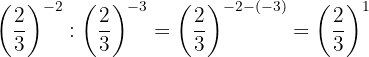
Por la propiedad 2 toda fracción elevada a la potencia uno, es igual a la misma fracción
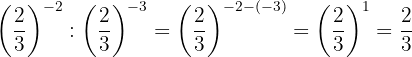
10
Tomamos la fracción inversa de la primera potencia para cambiar el signo del exponente

Las potencias tienen la misma base, entonces por la propiedad 4 la base es la misma y se restan los exponentes
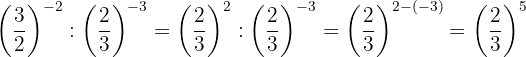
11
Se trata de la potencia de una potencia, entonces por la propiedad 5 la base es la misma y se multiplican los exponentes
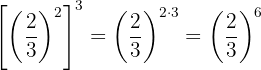
12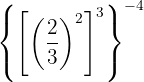
Se trata de la potencia de una potencia, entonces por la propiedad 5 la base es la misma y se multiplican los exponentes
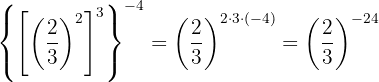
Para quitar el signo negativo del exponente, tenemos que escribir la fracción inversa
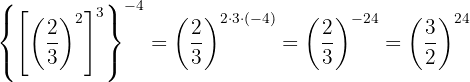
13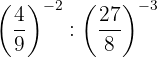
Descomponemos los números en factores y aplicamos la propiedad 5 de potencia de una potencia

Tomamos la fracción inversa de la primera potencia para cambiar el signo del exponente y aplicamos la propiedad 4 de cociente de potencias

14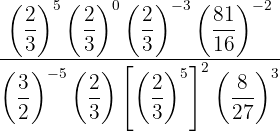
Trataremos de poner todas las fracciones con el mismo numerador y denominador, para ello descomponemos en factores los números que no sean primos

Se tienen elementos que son potencias de potencias, por lo que aplicamos la propiedad 5 par escribirlos como una sola potencia

Para las potencias con base  y exponentes negativos, ponemos la fracción inversa con exponente positivo
y exponentes negativos, ponemos la fracción inversa con exponente positivo

Tanto en el numerador como en el denominador multiplicamos las potencias con la misma base empleando la propiedad 3 y dividimos los resultados empleando la propiedad 4. Finalmente, ponemos la fracción inversa con exponente positivo














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar la fracción generatriz de los siguientes números decimales con periodo mixto
1)7,623
2)7,623
3)7623
4)*)4,165
5555(234:53-78×5)+66666:66(446-55×4)×56
Quien me ayuda??
14+ (3+8+5):2: [4+/32-20):4] = ayudaaa
el mcm del ejercicio del ejercicio 7 de vida diaria es 60 y no 120
Ya se corrigió.
Revisar el resultado del ejercicio 7 de Problemas de la vida diaria usando fracciones, el mcm de 4,5,6 y 10 es 60 y no 120
Ya se corrigió.
operaciones con fracciones con 3 fracciones con estos numeros 10/3+ 1/5 + 3/2