Temas
Recordemos que una inecuación es una desigualdad algebraica, es decir, es una expresión algebraica separada por el signo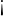 
(menor que), 
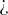(mayor que), 
(menor o igual que) o 
(mayor o igual que).
En este caso analizaremos las inecuaciones cuadráticas o de segundo grado de la forma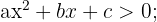 
con 
y 
números reales y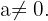 
Procedimiento para la resolución de una inecuación cuadrática
Procederemos a resolver la ecuación cuadrática 
considerando la siguiente serie de pasos.
1Igualar el primer miembro a cero y calcular las raíces de la ecuación cuadrática asociada
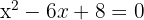
En este caso, el método más inmediato es el de factorización:
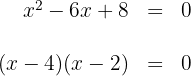
Igualamos cada factor a cero y obtenemos las raíces
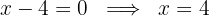
Nota: Este primer paso, el obtener las raíces de la ecuación cuadrática asociada, también se le conoce como obtener los valores críticos de la inecuación.
2Representar estos valores en la recta real
La recta real queda dividida en tres intervalos a partir de los valores 
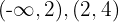y 
: 
y 
.
Se toma un punto de cada intervalo y se evalúa en la inecuación cuadrática para conocer el signo de cada intervalo. Por ejemplo, la triada de valores 
Nota: En caso de que la inecuación estuviera representada por los signos menor o igual que, o bien, mayor o igual que, los intervalos de los extremos deberían ser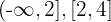 
y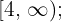 
es decir, deberán incluir a los extremos de los intervalos, convirtiéndose en intervalos cerrados o semi cerrados.
3Análisis del signo de los valores y de la expresión cuadrática
La solución está compuesta por aquellos intervalos que tengan el mismo signo que la expresión cuadrática. En este caso, la expresión es positiva porque se lee en la inecuación "la expresión algebraica es mayor que cero".
Por tanto, la solución de la inecuación cuadrática es el conjunto de intervalos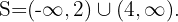 
Casos espaciales en la resolución de inecuaciones cuadráticas
Una inecuación formada por un binomio al cuadrado
A continuación se analizará la inecuación 
Aplicando el método de factorizaciónse obtiene
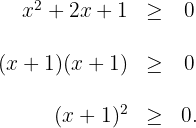
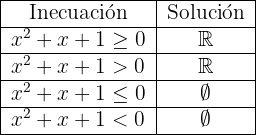
Como cualquier número real elevado al cuadrado siempre es positivo, siempre que una inecuación positiva y asociada al signo corresponda a un binomio al cuadrado, su solución será toda la recta real: 
.
En caso de que la inecuación esté relacionada con otros signos de desigualdad, las soluciones se siguen de la siguiente tabla:
Una inecuación sin puntos críticos
Se analizará la inecuación 
Su ecuación cuadrática asociada es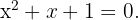 
Una manera de conocer cuántas soluciones tiene una ecuación cuadrática es calculando el discriminante 
1 Si este valor es positivo la ecuación tendrá dos raíces
2 Si este valor es cero tendrá sólo una raíz
3 Si este valor es negativo, no tendrá solución.
Calculamos el discriminante empleando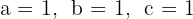 
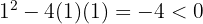
Entonces la inecuación no tiene puntos críticos y, por tanto, la recta numérica no se divide.
Debido a esto, la inecuación puede tener como solución a todos los números reales o ninguna solución; si el signo del término cuadrático no coincide con el de la desigualdad, no tiene solución.
Ejercicios de inecuaciones cuadráticas
1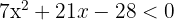
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
Igualando los factores a cero, se obtienen las raíces 
2 Representar los valores críticos en la recta numérica
Como las raíces son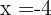 
y 
, la recta real se divide en los intervalos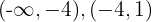 
y 
Tomando los valores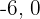 
y 
y los evaluamos en la inecuación
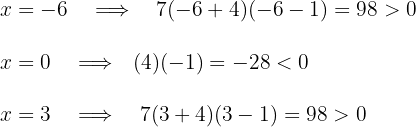
Como la expresión cuadrática es negativa, la solución es el intervalo 
2
1 Obtener los valores críticos de la inecuación
Como no puede factorizarse como el producto de dos binomios, se calcula el valor del discriminante:
2 Como el discriminante es negativo, la inecuación o no tiene soluciones o son todos los números reales.
Ya que el signo del término cuadrático coincide con el de la desigualdad (negativo-menor que), la solución de la inecuación son todos los números reales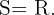 
3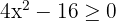
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
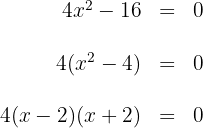
Igualando los factores a cero, se obtienen las raíces 
. Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
2 Representar los valores críticos en la recta numérica
Como las raíces son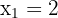 
y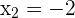 
, la recta real se divide en los intervalos 
y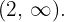 
Tomando los valores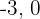 
y y los evaluamos en la inecuación
Ya que la expresión cuadrática es positiva, la solución de la inecuación es la unión de dos intervalos: 
4
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
Igualando el factor a cero, se obtiene la raíz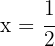 
2 Como el binomio al cuadrado es negativo y el signo es menor o igual que, la inecuación tiene una única solución: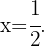 
5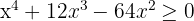
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
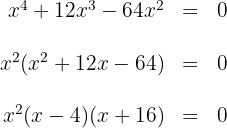
Igualando los factores a cero se obtienen las raíces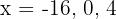 
. Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
2 Representar los valores críticos en la recta numérica
Como las raíces son 
y 
, la recta real se divide en los intervalos 
y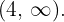 
Tomando los valores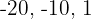 
y 
y los sustituimos en la inecuación
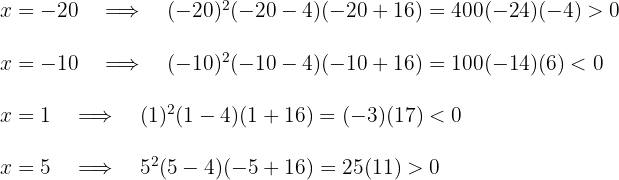
Como la expresión cuadrática es positiva, la solución es la unión de los intervalos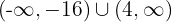 
y los valores críticos. Así, la solución es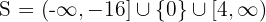 
6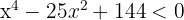
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
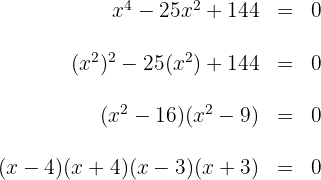
Igualando los factores a cero se obtienen las raíces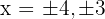 
.
2 Representar los valores críticos en la recta numérica
Como las raíces son 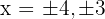, la recta real se divide en los intervalos 
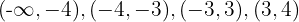y
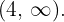
Tomando los valores 
y y los sustituimos en la inecuación
Como la expresión cuadrática es negativa, la solución es la unión de los intervalos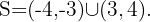 
7
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
Como el binomio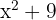 
siempre es mayor a cero para cualquer valor de 
, únicamente se consideran los binomios lineales para calcular los valores críticos. Así, 
son las raíces buscadas. Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
2 Representar los valores críticos en la recta numérica
Como las raíces son , la recta real se divide en los intervalos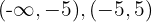 
y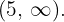 
Tomando los valores 
y 
, sustituimos en la inecuación
Como la expresión cuadrática es positiva o cero, la solución es la unión de los intervalos y los valores críticos, esto es,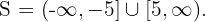 
¿Qué tal si buscas un profe mates?
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
INECUACION CUADRATICA RESOLVER x^2 − 4x + 7 > 0
Necesito ayuda con este problema 2x<(2x+1)(x-2)-2x(x-7)
Xfi
Por favor ayúdenme con este ejercicio que hay que resolver por medio de inecuaciones.
En un depósito cada tanque de leche tiene una capacidad de 200 litros. ¿Cuál es la cantidad máxima de tanques que puede cargar un camión cuya capacidad es de 50000 litros de leche?
necesito ayuda con esta inecuacion cuadratica: -2x al cuadrado +18x-36>0
×-18al cuadrado mas o menos√18al cuadrado-4(-2)(-36) dividido entre2×(-2)
×18mas o menos√18+-144. Dividido por-4
×18mas o menos√-126÷-4
×18+63/-4. × 18+63/-4. ×18-63)-4
×81/-4. ×-45/-4
×=-20,25. ×=11,25
Deberías hacer una tabla de valores para poder estudiar el signo y después escoger las soluciones adecuadas
Necesito q me respondan a esta ecuación
X²(x+4)
______>0
(X+1)(x+2)