Temas
La desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
La desviación típica se representa por  .
.
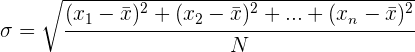

Ejemplo
Calcular la desviación típica de la distribución:
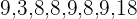
Calculamos la media aritmética
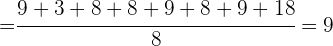
Sustituimos en la fórmula de la desviación típica
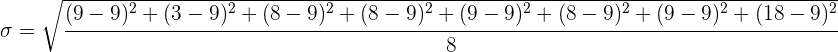


Desviación típica para datos agrupados
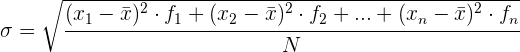
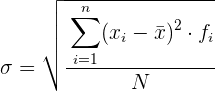
Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.
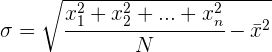
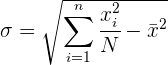
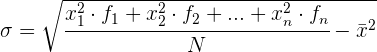
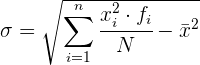
Ejemplo
Calcular la desviación típica de la distribución de la tabla:
 |  |  |  | |
|---|---|---|---|---|
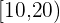 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
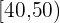 |  |  |  | 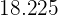 |
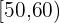 |  |  |  | 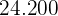 |
 |  |  |  | 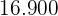 |
 |  |  |  | 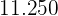 |
 |  |  |
Hemos añadido la columna  porque queremos hallar su sumatoria
porque queremos hallar su sumatoria 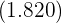 , que después dividiremos por
, que después dividiremos por 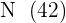 para obtener la media
para obtener la media
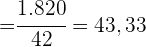
Hemos añadido la columna  porque queremos hallar su sumatoria
porque queremos hallar su sumatoria  , que después dividiremos por
, que después dividiremos por 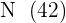 y al resultado le restaremos la media aritmética al cuadrado
y al resultado le restaremos la media aritmética al cuadrado 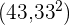 , y por último haremos la raíz cuadrada del resultado obtenido
, y por último haremos la raíz cuadrada del resultado obtenido
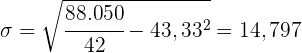
Propiedades de la desviación típica
1 La desviación típica será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
2 Si a todos los valores de la variable se les suma un número la desviación típica no varía.
3 Si todos los valores de la variable se multiplican por un número la desviación típica queda multiplicada por dicho número.
4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones típicas se puede calcular la desviación típica total.
Si todas las muestras tienen el mismo tamaño:

Si las muestras tienen distinto tamaño:
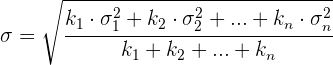
Observaciones sobre la desviación típica
1 La desviación típica, al igual que la media y la varianza, es un índice muy sensible a las puntuaciones extremas.
2 En los casos que no se pueda hallar la media tampoco será posible hallar la desviación típica.
3 Cuanta más pequeña sea la desviación típica mayor será la concentración de datos alrededor de la media.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Media de 30. 35. 30. 40. 35. 30. 35.
suma los datos y nos da 235 a eso le dividimos el numero de datos que es 7 se divide 235 entre 7 =33.5 esa es la media o el promedio
Que tanto% de las inversiones establecidas por el empresario entran comprendidas a más de 3.5 desviaciones estándar y a menos de 3.5 desviaciones estándar respecto a la media según el teorema de Chevichev
Segun chevichev seria un 35% al dividirlo entre cien y calculandolo en porcenteaje con la regla de Evalis
Me pueden ayudar por favor.
Necesito determinar la desviación media del siguiente grupo de números en relación al total de las observaciones: 10, 8, 7, 9, 6.
Gracias.):
Al calcular la media y la desviación estándar de 50 datos, ambos resultaron ser iguales a 12. Un chequeo de los datos mostró que en lugar de un dato con valor de 12,8 se había introducido 17,8; corrija la media y la desviación estándar.
Desviación y varianza y tipica12..6..7.3.15.10.18.5