Temas

Atendiendo al número de sus soluciones
Sistema compatible determinado
Es un sistema que tiene una sola solución.
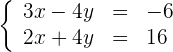
Gráficamente la solución es el punto de corte de las dos rectas.

Sistema compatible indeterminado
Es un sistema que tiene infinitas soluciones.
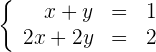
Gráficamente obtenemos dos rectas coincidentes. Cualquier punto de la recta es solución.

Sistema incompatible
Es un sistema que no tiene solución

Gráficamente obtenemos dos rectas paralelas.
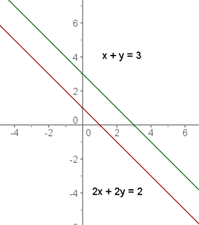
Sistemas de ecuaciones equivalentes
Los sistemas de ecuaciones equivalentes son los que tienen la misma solución, aunque tengan distinto número de ecuaciones.
Obtenemos sistemas equivalentes por eliminación de ecuaciones dependientes, si:
1 Todos los coeficientes son ceros.
2Dos filas son iguales.
3Una fila es proporcional a otra.
4Una fila es combinación lineal de otras.
Criterios de equivalencia de sistemas de ecuaciones
1 Si a ambos miembros de una ecuación de un sistema se les suma o se les resta una misma expresión, el sistema resultante es equivalente.
2 Si multiplicamos o dividimos ambos miembros de las ecuaciones de un sistema por un número distinto de cero, el sistema resultante es equivalente.
3 Si sumamos o restamos a una ecuación de un sistema otra ecuación del mismo sistema, el sistema resultante es equivalente al dado.
4 Sin en un sistema se sustituye una ecuación por otra que resulte de sumar las dos ecuaciones del sistema previamente multiplicadas o divididas por números no nulos, resulta otro sistema equivalente al primero.
5 Si en un sistema se cambia el orden de las ecuaciones o el orden de las incógnitas, resulta otro sistema equivalente.
Sistemas de ecuaciones escalonados
Son aquellos en que cada ecuación tiene una incógnita menos que la anterior.

Si nos vamos a la tercera ecuación, tenemos que  .
.
Sustituyendo su valor en la segunda ecuación obtenemos que  .
.
Y sustituyendo en la primera ecuación los valores anteriores tenemos que 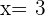 .
.
También es un sistema escalonado:
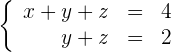
Como en este caso tenemos más incógnitas que ecuaciones, tomaremos una de las incógnitas (por ejemplo la  ) y la pasaremos al segundo miembro.
) y la pasaremos al segundo miembro.

Consideraremos 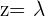 , siendo
, siendo  un parámetro que tomara cualquier valor real.
un parámetro que tomara cualquier valor real.
Así, las soluciones son:
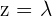
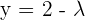
 .
.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
2x+3y=
X-y=1
Me podría ayudar con este ejercicio
3X+2y=3
-X+5y=16
Hola, me puede ayudar con esta ecuación de métodos igualación:
Y=2x+12
5x+3y=-19