Temas
Antes que todo establezcamos cierta notación alterna para las derivadas de una función  .
.
La razón de establecer notaciones alternas para el mismo concepto, es porque hay ocasiones en que los desarrollos son muy grandes o complicados, y es necesario para que sea más práctico que se hagan menos extensas las notaciones, ya que aquí lo importante es que sigan representando el mismo concepto.
La primer derivada de una función tiene las tres notaciones que tenemos aquí:
y la segunda derivada de una función (la derivada de la derivada), tiene las siguientes notaciones alternas:
en este caso por términos de claridad ocuparemos para la primer derivada, a la notación 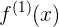 , y para la segunda derivada
, y para la segunda derivada 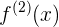 .
.
Una vez establecida la notación que usaremos, comentemos acerca de ciertas características que podemos estudiar de las funciones.
Hablando de forma más precisa, conozcamos los criterios que nos informan dónde una función adquiere su máximo o mínimo valor posible dentro de una región establecida, razón por la cual se llaman máximo o mínimo relativos.
Repasa los máximos y mínimos de funciones con clases particulares matematicas de Superprof.

Extremos relativos
Antes que todo identifiquemos el tipo de punto que deseamos localizar, en términos simples se trata de puntos donde una función adquiere un máximo o mínimo valor posible, esto es en comparación a los puntos de un entorno cercano a ellos, a este tipo de puntos los llamaremos extremos relativos.
Si 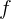 es una función derivable en
es una función derivable en 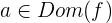 , entonces
, entonces  es un extremo relativo o local si:
es un extremo relativo o local si:
Máximos relativos
Si 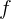 es una función derivable en
es una función derivable en 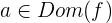 , entonces
, entonces  es un máximo relativo o local si:
es un máximo relativo o local si:
Mínimos relativos
Si 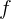 es una función derivable en
es una función derivable en 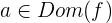 , entonces
, entonces  es un mínimo relativo o local si:
es un mínimo relativo o local si:
Cálculo de máximos y mínimos
Consideremos a la siguiente función 
Para hallar los extremos locales seguiremos los siguientes pasos:
1Hallamos la primera derivada de la función y calculamos sus raíces.
Primero la derivada de la función

Ahora sus raíces, resolviendo la ecuación

Entonces sus raíces son

2Realizamos la segunda derivada, y calculamos el signo que toman en ella las raíces.
Calculemos la segunda derivada de la función

Evaluemos las raíces obtenidas en la segunda derivada
 ,
,  en
en  la función tiene un máximo relativo
la función tiene un máximo relativo
 ,
,  en
en  la función tiene un mínimo relativo
la función tiene un mínimo relativo
3Calculamos la imagen (en la función) de los extremos relativos.
 ,
, en
en  la gráfica de la función tiene un máximo relativo
la gráfica de la función tiene un máximo relativo
 ,
,  en
en  la gráfica de la función tiene un mínimo relativo
la gráfica de la función tiene un mínimo relativo
¿Vives en la capital? ¡Échale un ojo a nuestras clases particulares matematicas madrid!
Estudio de los extremos relativos a partir del crecimiento
Si ya hemos estudiado el crecimiento y decrecimiento de una función habrá:
- Un máximo en el punto de la función cuando esta pasa de creciente
 a decreciente
a decreciente  .
.
- Un mínimo en el punto de la función cuando esta pasa de decreciente
 a creciente
a creciente  .
.
Ejemplo:
Consideremos a la siguiente función 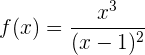
Para hallar los extremos locales seguiremos los siguientes pasos:
1Hallamos el dominio de la función, la primera derivada y calculamos sus raíces.
Primero el dominio de la función
Busquemos los puntos donde se indetermina la función, es decir, valores donde 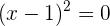
.
Dicho valor es  , es el valor que debemos quitar, por lo tanto
, es el valor que debemos quitar, por lo tanto 
.
Ahora calculemos la derivada de la función

Ahora sus raíces, resolviendo la ecuación
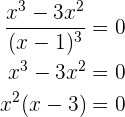
Sus raíces son

2Tomamos a los valores calculados y generamos a sectores de la recta real.
Después tomamos a un valor de cada sector, lo evaluamos en la primer derivada y observamos los signos obtenidos, con la finalidad de analizar la naturaleza de la función en cada sector.
Tomamos a los valores calculados y generamos a sectores de la recta real
Los valores son 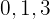 entonces los sectores son
entonces los sectores son 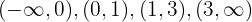
Evaluemos un elemento de cada sector en la primer derivada
- Sea
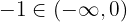 , entonces
, entonces 
 en
en  la función es creciente
la función es creciente 
- Sea
 , entonces
, entonces 
 en
en 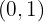 la función es creciente
la función es creciente 
- Sea
 , entonces
, entonces 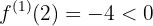
 en
en 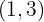 la función es decreciente
la función es decreciente 
- Sea
 , entonces
, entonces 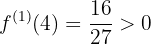
 en
en 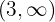 la función es creciente
la función es creciente 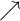
En la siguiente tabla podemos ver la información obtenida:
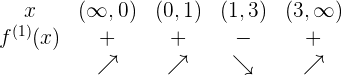
3Interpretamos la información e identificamos los máximo o mínimos.
Observamos que se generan dos cambios de signo, el que se encuentra de 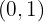 a
a 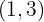 lo descartamos porque ahí se tiene la indeterminación.
lo descartamos porque ahí se tiene la indeterminación.
El siguiente cambio de signo es de 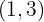 a
a 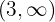 , y como es de decrecente a creciente entonces en
, y como es de decrecente a creciente entonces en 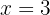 se tiene un mínimo relativo
se tiene un mínimo relativo
4Evaluar el número en la función para conocer el punto del plano.
Vemos que 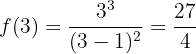 , entonces en el punto
, entonces en el punto  , la función tiene un mínimo relativo.
, la función tiene un mínimo relativo.
Ejercicios para practicar
Consideremos a la siguiente función 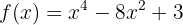
1Hallamos la primera derivada de la función y calculamos sus raíces.
Primero la derivada de la función
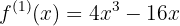
Ahora sus raíces, resolviendo la ecuación

Sus raíces son

2Realizamos la segunda derivada, y calculamos el signo que toman en ella las raíces.
Calculemos la segunda derivada de la función
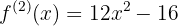
Evaluemos las raíces obtenidas en la segunda derivada
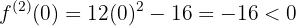 ,
,  en
en  la función tiene un máximo relativo
la función tiene un máximo relativo
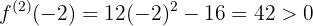 ,
,  en
en  la función tiene un mínimo relativo
la función tiene un mínimo relativo
 ,
,  en
en  la función tiene un mínimo relativo
la función tiene un mínimo relativo
3Calculamos la imagen (en la función) de los extremos relativos.
 ,
,  en
en  la gráfica de la función tiene un mínimo relativo
la gráfica de la función tiene un mínimo relativo
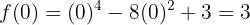 ,
, en
en 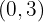 la gráfica de la función tiene un máximo relativo
la gráfica de la función tiene un máximo relativo
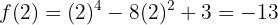 ,
,  en
en  la gráfica de la función tiene un mínimo relativo
la gráfica de la función tiene un mínimo relativo
Consideremos a la siguiente función 
1Hallamos la primera derivada de la función y calculamos sus raíces.
Primero la derivada de la función
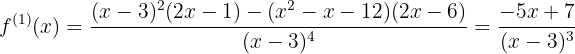
Ahora sus raíces, resolviendo la ecuación
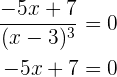
significa que su raíz es
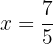
2Realizamos la segunda derivada, y calculamos el signo que toman en ella las raíces.
Calculemos la segunda derivada de la función

Evaluemos la raíz obtenida en la segunda derivada
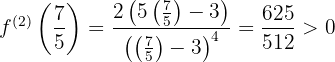 ,
,  en
en 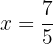 la función tiene un mínimo relativo
la función tiene un mínimo relativo
3Calculamos la imagen (en la función) de los extremos relativos.
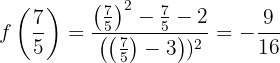
 en
en 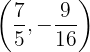 la gráfica de la función tiene un mínimo relativo
la gráfica de la función tiene un mínimo relativo
Consideremos a la siguiente función 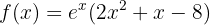
1Hallamos la primera derivada de la función y calculamos sus raíces.
Primero la derivada de la función

Ahora sus raíces, resolviendo la ecuación

significa que sus raíces son
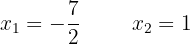
2Realizamos la segunda derivada, y calculamos el signo que toman en ella las raíces.
Calculemos la segunda derivada de la función
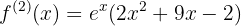
Evaluemos las raíces obtenidas en la segunda derivada
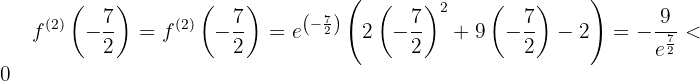 ,
,  en
en 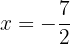 la función tiene un máximo relativo
la función tiene un máximo relativo
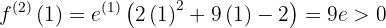 ,
,  e en
e en  la función tiene un mínimo relativo
la función tiene un mínimo relativo
3Calculamos la imagen (en la función) de los extremos relativos.
 ,
,  en
en 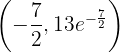 la gráfica de la función tiene un máximo relativo
la gráfica de la función tiene un máximo relativo
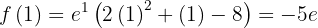 ,
,  en
en 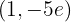 la gráfica de la función tiene un mínimo relativo
la gráfica de la función tiene un mínimo relativo
Consideremos a la siguiente función 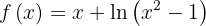 .
.
En este caso es necesario tener presente su dominio, ya que es posible que debamos descartar valores por no pertenecer a él.
De hecho siempre se debe de hacer, pero no se hace cuando se tiene claro cuál es el dominio.
0Hallamos el dominio de la función
El dominio de la función logaritmo natural, es cuando el argumento es positivo, entonces debemos resolver 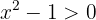
Las soluciones de 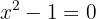 son
son 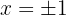 . Significa que debemos generar los sectores
. Significa que debemos generar los sectores 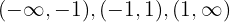 , y de ahí tomar a un número de cada sector, evaluarlo en
, y de ahí tomar a un número de cada sector, evaluarlo en 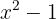 y conocer el signo generado, para finalmente resolver.
y conocer el signo generado, para finalmente resolver.

Significa que la solución de la desigualdad, por lo tanto el dominio de la función es 
1Hallamos la primera derivada de la función y calculamos sus raíces.
Primero la derivada de la función
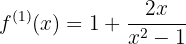
Ahora sus raíces, resolviendo la ecuación
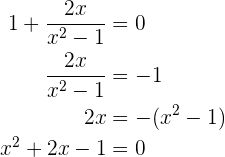
Sus raíces son

Descartamos a 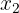 ya que
ya que 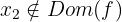
2Realizamos la segunda derivada, y calculamos el signo que toman en ella las raíces.
Calculemos la segunda derivada de la función
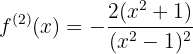
Evaluemos las raíces obtenidas en la segunda derivada
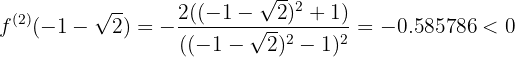 ,
,  en
en 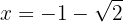 la función tiene un máximo relativo
la función tiene un máximo relativo
3Calculamos la imagen (en la función) de los extremos relativos.
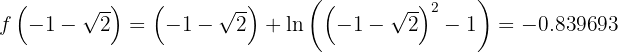 ,
, en
en  la gráfica de la función tiene un máximo relativo
la gráfica de la función tiene un máximo relativo
Consideremos a la siguiente función 
1Hallamos la primera derivada de la función y calculamos sus raíces.
Primero la derivada de la función
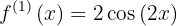
Ahora sus raíces, resolviendo la ecuación
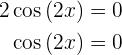
Sus raíces son
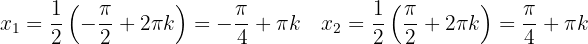 , con
, con 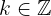
2Realizamos la segunda derivada, y calculamos el signo que toman en ella las raíces.
Calculemos la segunda derivada de la función

Evaluemos las raíces obtenidas en la segunda derivada
 ,
,  en
en  la función tiene un mínimo relativo para cada
la función tiene un mínimo relativo para cada 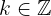
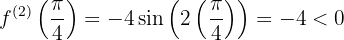 ,
,  en
en 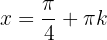 la función tiene un máximo relativo para cada
la función tiene un máximo relativo para cada 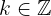
3Calculamos la imagen (en la función) de los extremos relativos.
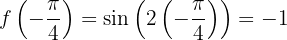 ,
,  en
en 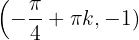 la gráfica de la función tiene un mínimo relativo relativo para cada
la gráfica de la función tiene un mínimo relativo relativo para cada 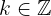
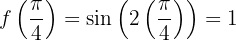 ,
,  en
en 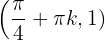 la gráfica de la función tiene un máximo relativo relativo para cada
la gráfica de la función tiene un máximo relativo relativo para cada 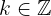
Problemas
Determinar  ,
, y
y  para que la función
para que la función 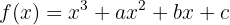 tenga un máximo para
tenga un máximo para 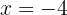 , un mínimo para
, un mínimo para  , y tome el valor
, y tome el valor 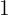 para
para  .
.
El problema se traduce a que ocurran las siguientes condiciones:
lo cual significa que debemos calcular a la primera derivada de la función

y con esto realizar las evaluaciones
generándose un sistema de ecuaciones tres por tres
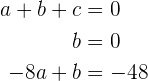
cuya solución es 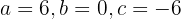
Determinar el valor de  ,
, ,
, y
y 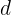 para que la función
para que la función 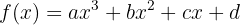 tenga un máximo en
tenga un máximo en  y un mínimo en
y un mínimo en 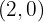 .
.
El problema se traduce a que ocurran las siguientes condiciones:
significa que debemos calcular a la primer derivada de la función

y entonces hacer las evaluaciones correspondientes
generando el siguiente sistema de ecuaciones cuatro por cuatro
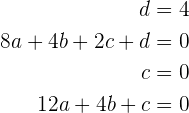
cuya solución es 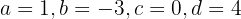
Dada la función: 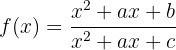
Calcula  ,
, y
y  , de modo que
, de modo que  tenga en
tenga en 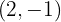 un extremo local y que la curva pase por el origen de coordenadas.
un extremo local y que la curva pase por el origen de coordenadas.
El problema se traduce a que ocurran las siguientes condiciones:
significa que debemos calcular a la primer derivada de la función
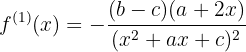
y entonces hacer las evaluaciones correspondientes
generando el siguiente sistema de ecuaciones tres por tres
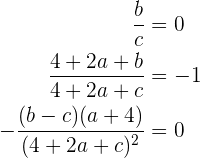
cuya solución es 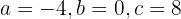
Hallar  y
y  para que la función:
para que la función: 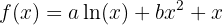 tenga extremos en los puntos
tenga extremos en los puntos 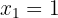 y
y 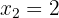 . Para esos valores de
. Para esos valores de  y
y  , ¿qué tipo de extremos tiene la función en
, ¿qué tipo de extremos tiene la función en 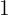 y en
y en 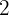 ?
?
Calculemos la primer y segunda derivada de la función, esto es para buscar las condiciones para que sean extremos y después para conocer su naturaleza.
Ahora como queremos que la función tenga extremos en los puntos 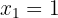 y
y 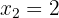 , se establecen las siguientes igualdades
, se establecen las siguientes igualdades
generando un sistema cuya solución es:  y
y 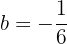 .
.
Ya encontramos los valores que provocan que la función tenga extremos en el lugar indicado, ahora veamos su naturaleza. Para esto necesitamos a la segunda derivada de la función:

Ahora veamos la naturaleza de cada extremo
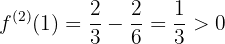 ,
,  en
en 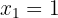 , la función tiene un mínimo relativo
, la función tiene un mínimo relativo
 ,
,  en
en 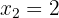 , la función tiene un máximo relativo
, la función tiene un máximo relativo
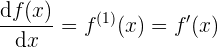
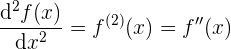










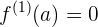

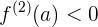
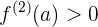
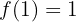
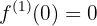
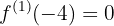

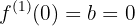

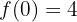

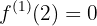
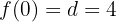

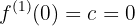
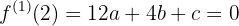
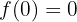

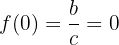



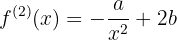
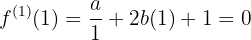
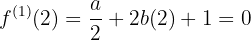



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3