Temas

Puntos de inflexión
Los puntos de inflexión de una función son aquellos puntos en los que la gráfica de la función cambia de concavidad, es decir, pasa de cóncava a convexa o viceversa. Informalmente hablando, podemos decir que es el momento en que la función cambia de tendencia.
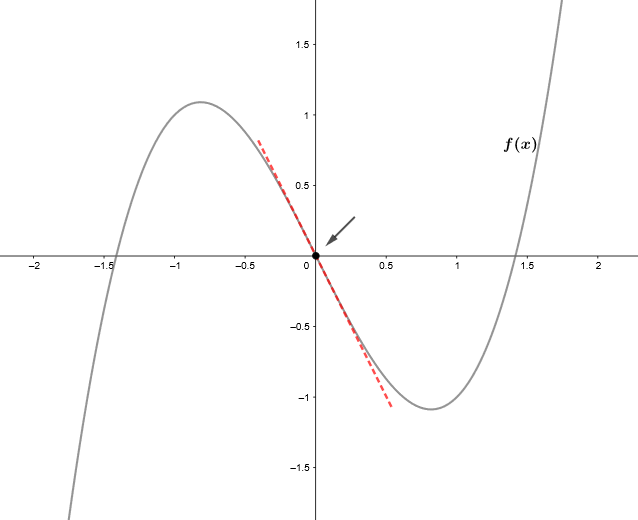
Encontrar los puntos de inflexión por medio del criterio de la tercera derivada
Para encontrar los puntos de inflexión de una función derivable  por medio del criterio de la tercera derivada realizamos los siguientes pasos.
por medio del criterio de la tercera derivada realizamos los siguientes pasos.
1 Encontramos la primera derivada de  :
:  .
.
2 Hallamos la segunda derivada de  e igualamos a cero:
e igualamos a cero:  .
.
3 Despejamos la variable independiente " " y encontramos los valores para los que se cumple la condición. Es decir, buscamos los
" y encontramos los valores para los que se cumple la condición. Es decir, buscamos los 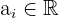 tales que
tales que 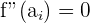 con
con  .
.
4 Hallamos la tercera derivada de  :
: 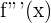 .
.
5 Sustituimos los 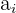 en la tercera derivada y si
en la tercera derivada y si  entonces se tiene un punto de inflexión en
entonces se tiene un punto de inflexión en 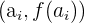 .
.
¿Buscas clases de matematicas a domicilio? ¡Están en Superprof!
Ejemplo: cálculo de puntos de inflexión utilizando el criterio de la tercera derivada.
Calcular los puntos de inflexión de:
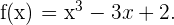
Solución:
1 Encontramos la primera derivada de 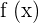 :
:
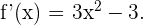
2 Hallamos la segunda derivada de  e igualamos a cero:
e igualamos a cero:
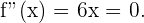
3 Encontramos las raíces de 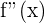 . Notemos que
. Notemos que
 es decir,
es decir, 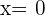 es raíz de
es raíz de 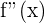 .
.
4 Hallamos la tercera derivada de  :
:
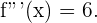
5 Sustituimos  en la tercera derivada:
en la tercera derivada:
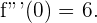
Dado que  tendremos que
tendremos que 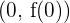 punto de inflexión, donde
punto de inflexión, donde
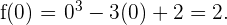 Esto es, el punto
Esto es, el punto  es un punto de inflexión.
es un punto de inflexión.
Cálculo de puntos de inflexión conociendo intervalos de concavidad y convexidad
Calculemos los puntos de inflexión de las siguientes funciones considerando los intervalos en los que es cóncava y en los que es convexa .
1 
Solución:
Comenzamos analizando el dominio de la función. Notemos que  no está definida cuando el denominador se hace cero, por lo que debemos descartar los valores que anulen el denominador,
no está definida cuando el denominador se hace cero, por lo que debemos descartar los valores que anulen el denominador,
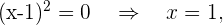
por tanto 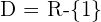 .
.
Continuemos calculando la primera y segunda derivada de  para encontrar posibles puntos de inflexión,
para encontrar posibles puntos de inflexión,

Igualamos la segunda derivada igual a cero:

Por lo tanto tenemos que un posible punto de inflexión es en 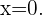
Ahora bien, hay una propiedad de la segunda derivada que nos dice que si la segunda derivada de  es positiva en un intervalo entonces
es positiva en un intervalo entonces  es convexa en ese intervalo y similarmente si la segunda derivada de
es convexa en ese intervalo y similarmente si la segunda derivada de  es negativa en un intervalo entonces
es negativa en un intervalo entonces  es cóncava en ese intervalo . Tomando esto en cuenta, revisamos los signos al segmentar el dominio:
es cóncava en ese intervalo . Tomando esto en cuenta, revisamos los signos al segmentar el dominio:
- Si
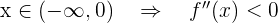
- Si
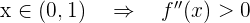
- Si
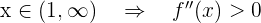 .
.
Luego, la función es cóncava en el intervalo  y convexa en
y convexa en  . Así, como la función pasa de cóncava a convexa en el punto
. Así, como la función pasa de cóncava a convexa en el punto  , entonces podemos afirmar que el punto
, entonces podemos afirmar que el punto 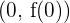 es un punto de inflexión. Esto es, en el punto
es un punto de inflexión. Esto es, en el punto  .
.
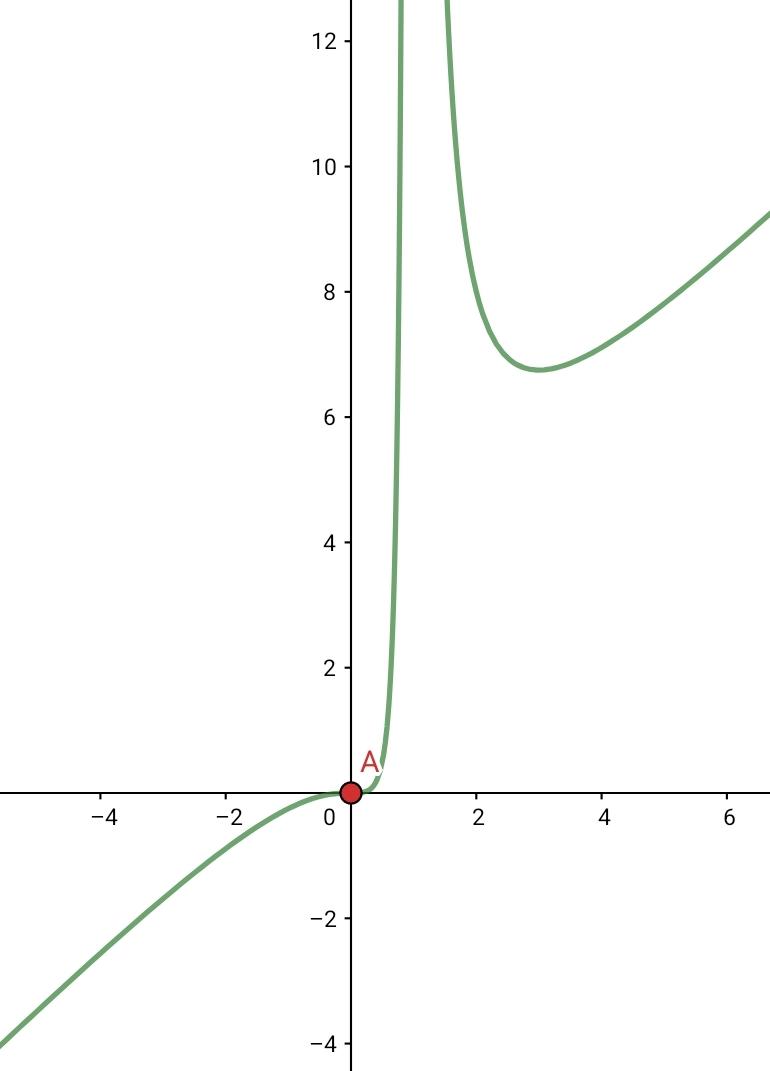

Solución:
 . Calculamos la primera y segunda derivada
. Calculamos la primera y segunda derivada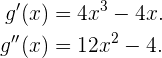
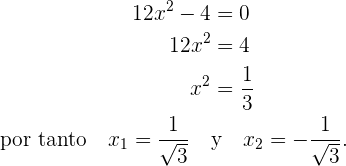 Ahora bien, tenemos que
Ahora bien, tenemos que - Si
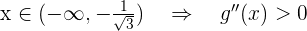 ,
, - Si
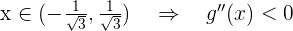 , y
, y - Si
 ,
,
Similar al ejercio anterior esto nos dice que  cambia de convexa a cóncava en
cambia de convexa a cóncava en  y de cóncava a convexa en
y de cóncava a convexa en  . Por lo que podemos concluir que sus puntos de inflexión son:
. Por lo que podemos concluir que sus puntos de inflexión son:
 , es decir, en el punto
, es decir, en el punto 
 , es decir, en el punto
, es decir, en el punto 

Problemas de puntos de inflexión
1 Obtener la ecuación de la recta tangente a la gráfica de 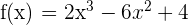 en su punto de inflexión.
en su punto de inflexión.
Solución:
Encontraremos primeramente el punto de inflexión de  , para esto empezamos calculando primera y segunda derivada de
, para esto empezamos calculando primera y segunda derivada de  :
:

Igualamos segunda derivada a cero y encontramos valor para el que se anula

Proseguimos calculando la tercera derivada de  y verificando que
y verificando que 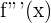 no se anula en
no se anula en 

Puesto que 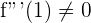 , entonces
, entonces 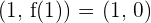 punto de inflexión.
punto de inflexión.
Ahora bien, encontraremos la ecuación de la recta tangente en el punto 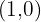 , para esto utilizaremos la forma punto-pendiente de la recta
, para esto utilizaremos la forma punto-pendiente de la recta
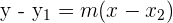
donde  punto de la recta y
punto de la recta y  pendiente de la recta.
pendiente de la recta.
La pendiente de la recta tangente en el punto 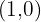 la encontramos con la primera derivada
la encontramos con la primera derivada

Por tanto la ecuación de la recta tangente es


2 La curva 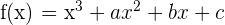 corta al eje de abscisas en
corta al eje de abscisas en  y tiene un punto de inflexión en
y tiene un punto de inflexión en  . Hallar
. Hallar  y
y  .
.
Solución:
Tenemos que 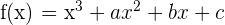 con derivadas
con derivadas
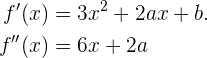
Ahora bien, sabemos que  corta al eje de las abscisas en
corta al eje de las abscisas en 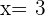 entonces
entonces
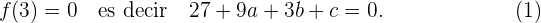
También sabemos que el punto de inflexión es en  por lo que la segunda derivada debe anularse en
por lo que la segunda derivada debe anularse en 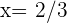 y
y 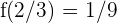 , es decir,
, es decir,


De (2) concluimos que  , y sustituyendo el valor de
, y sustituyendo el valor de  en (1) y (3) tendremos que
en (1) y (3) tendremos que


Obteniendo así un sistema de ecuaciones lineales  :
:
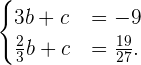
Resolvemos dicho sistema utilizando cualquier método de su preferencia y obtenemos que

3 Determina las ecuaciones de la tangente y normal en su punto de inflexión a la curva: 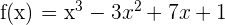 .
.
Solución:
Procedemos similarmente al problema 1, pero esta vez considerando que la ecuación de la recta normal en un punto  es
es

Comenzamos buscando el punto de inflexión de  y para esto calculamos la primera y segunda derivada
y para esto calculamos la primera y segunda derivada
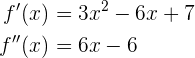
Igualamos segunda derivada a cero y encontramos raíz
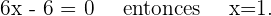
Calculamos tercera derivada y verificamos que no se anule en 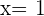
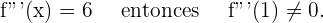
Entonces 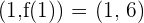 punto de inflexión.
punto de inflexión.
Ahora bien, 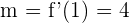 entonces
entonces
Recta tangente : 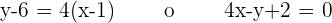
Recta normal : 
4 Sea 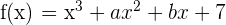 . Hallar
. Hallar  y
y  de manera que la gráfica de la función
de manera que la gráfica de la función  tenga para
tenga para 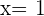 un punto de inflexión, y cuya recta tangente en ese punto forme un ángulo de
un punto de inflexión, y cuya recta tangente en ese punto forme un ángulo de 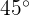 con el eje
con el eje 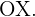
Solución:
Empezamos calculando primera y segunda derivada

Puesto que queremos un ángulo de 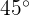 con el eje
con el eje  en el punto de inflexión se debe tener que
en el punto de inflexión se debe tener que
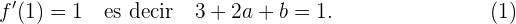
y además queremos un punto de inflexion en 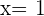 entonces
entonces
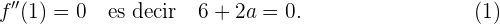
Resolvemos el sistema de ecuaciones formado por (4) y (5), y obtenemos que

Resuelve todas tus dudas con un profesor mates.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4