Temas
En este artículo vamos a representar gráficamente la función

estudiando los siguientes puntos:

Dominio
Dado que la función en cuestión es una función racional, entonces el dominio de la función serán todo los números reales menos aquellos puntos donde el denominador se anula, es decir, menos aquellos puntos donde la función no existe. Así, hacemos
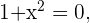
la cual no tiene solución en  . Por lo tanto el dominio de la función es:
. Por lo tanto el dominio de la función es: 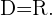
Simetría
Nótese que  es decir, la función es impar. Por lo tanto tenemos simetría respecto al origen.
es decir, la función es impar. Por lo tanto tenemos simetría respecto al origen.
Puntos de corte con los ejes
- Puntos de corte con el eje
 : Para encontrar estos puntos debemos hacer
: Para encontrar estos puntos debemos hacer 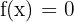 y resolver. Esto es,
y resolver. Esto es,
 Por lo tanto el único punto de corte con el eje
Por lo tanto el único punto de corte con el eje  es
es  .
. - Puntos de corte con el eje
 : Para encontrar estos puntos debemos hacer
: Para encontrar estos puntos debemos hacer  y ver cuál es el valor de la función
y ver cuál es el valor de la función

Así, el único punto de corte con el eje es
es  .
.
Asíntotas
- Asíntotas horizontales: Observe que
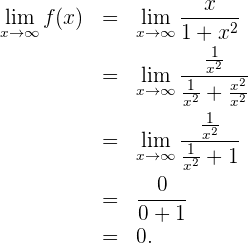 Así, la recta
Así, la recta  , es la única asíntota horizontal puesto que también se tiene que
, es la única asíntota horizontal puesto que también se tiene que 
- Asíntotas verticales: Ya que el dominio de la función es
 , entonces la función no tiene asíntotas verticales.
, entonces la función no tiene asíntotas verticales. - Asíntotas oblicuas: Debido a que la función presenta al menos una asíntota horizontal, entonces la función no tiene asíntotas oblicuas.
Crecimiento y decrecimiento
Primero encontramos la primera derivada, la igualamos a cero y despejamos 
 Luego se tiene que
Luego se tiene que

Por lo tanto los puntos críticos de la función ocurren cuando  Ahora revisamos los signos al segmentar el dominio:
Ahora revisamos los signos al segmentar el dominio:



De aquí obtenemos que la función es:
- Creciente en
 .
. - Decreciente en
 .
.
Mínimos y máximos
Para encontrar los mínimos y máximos debemos calcular la segunda derivada y evaluarla en los puntos críticos. Tenemos que, la segunda derivada de la función es:
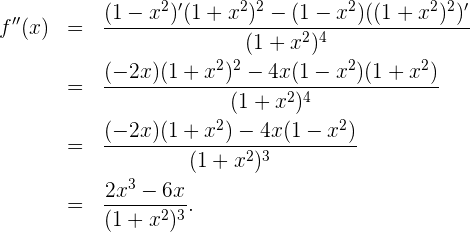
Luego, evaluamos la segunda derivada en los puntos críticos 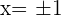 encontrados anteriormente.
encontrados anteriormente.
- En
 , tenemos que
, tenemos que

Así, como , entonces sabemos que el punto
, entonces sabemos que el punto 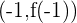 es un mínimo, esto es, tenemos un mínimo en el punto
es un mínimo, esto es, tenemos un mínimo en el punto  .
. - En
 , tenemos que
, tenemos que
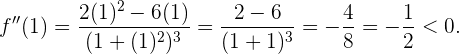
Así, como , entonces sabemos que el punto
, entonces sabemos que el punto 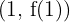 es un máximo, esto es, tenemos un máximo en el punto
es un máximo, esto es, tenemos un máximo en el punto  .
.
Concavidad y convexidad
Para determinar la concavidad y convexidad debemos hacer  y resolver para
y resolver para  :
:

Es decir, 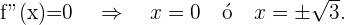
Ahora revisamos los signos de 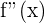 al segmentar el dominio con estos puntos:
al segmentar el dominio con estos puntos:
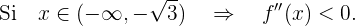
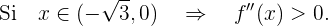


Pero sabemos que, si 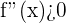 en un intervalo, entonces la función
en un intervalo, entonces la función  es convexa en ese intervalo. De igual manera, si
es convexa en ese intervalo. De igual manera, si 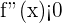 en un intervalo, entonces la función
en un intervalo, entonces la función  es cóncava en ese intervalo.
es cóncava en ese intervalo.
Entonces tenemos que la función es
- Convexa en
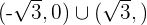 .
. - Cóncava en
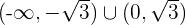 .
.
Puntos de inflexión
Para encontrar los puntos de inflexión haremos uso del criterio de la tercera derivada ( ver: ¿Qué son los puntos de inflexión?). Tenemos que
 Ahora, evaluamos
Ahora, evaluamos 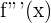 en los puntos
en los puntos  y
y 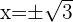 que corresponden a los valores que obtuvimos al hacer
que corresponden a los valores que obtuvimos al hacer  y continuando con el criterio de la tercera derivada, si
y continuando con el criterio de la tercera derivada, si  , donde
, donde  denota cualquiera de los tres puntos anteriores, entonces tenemos un punto de inflexión en
denota cualquiera de los tres puntos anteriores, entonces tenemos un punto de inflexión en 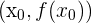 . Sustituyendo:
. Sustituyendo:
- Si
 , entonces
, entonces

Luego, tenemos un punto de inflexión en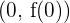 , es decir, en
, es decir, en  .
. - Si
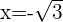 , entonces
, entonces
 Luego, tenemos un punto de inflexión en
Luego, tenemos un punto de inflexión en 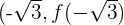 , es decir, en
, es decir, en  .
. - Si
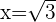 , entonces
, entonces

Luego, tenemos un punto de inflexión en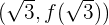 , es decir, en
, es decir, en
 .
.
Representación gráfica
La gráfica de la función se representa en la siguiente figura:

Para ver más ejemplos como este, visitar:












Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3