Temas
Función real de variable real es toda correspondencia  que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real.
que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real.
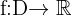

El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por  .
.
El número  perteneciente al dominio de la función recibe el nombre de variable independiente.
perteneciente al dominio de la función recibe el nombre de variable independiente.
Al número,  , asociado por
, asociado por  al valor
al valor  , se le llama variable dependiente. La imagen de
, se le llama variable dependiente. La imagen de  se designa por
se designa por  . Luego
. Luego

Se denomina recorrido de una función al conjunto de los valores reales que toma la variable  o
o 
Dominio de una función
Dominio de la función polinómica entera
El dominio es  , cualquier número real tiene imagen.
, cualquier número real tiene imagen.
Dominio de la función racional
El dominio es  menos los valores que anulan al denominador (no puede existir un número cuyo denominador sea cero).
menos los valores que anulan al denominador (no puede existir un número cuyo denominador sea cero).
Dominio de la función irracional de índice impar
El dominio es  .
.
Dominio de la función irracional de índice par
El dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
Dominio de la función logarítmica
El dominio está formado por todos los valores que hacen que el argumento del logaritmo sea mayor que cero.
Dominio de la función exponencial
El dominio es  .
.
Dominio de la función seno
El dominio es  .
.
Dominio de la función coseno
El dominio es  .
.
Dominio de la función tangente
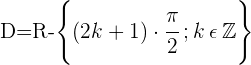
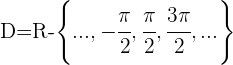
Dominio de la función cotangente


Dominio de la función secante
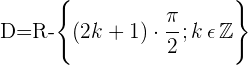
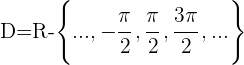
Dominio de la función cosecante
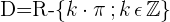
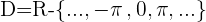
Dominio de operaciones con funciones


Gráfica de funciones
Si  es una función real, a cada par
es una función real, a cada par 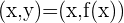 determinado por la función
determinado por la función  le corresponde en el plano cartesiano un único punto
le corresponde en el plano cartesiano un único punto 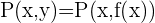 . El valor de
. El valor de  debe pertenecer al dominio de definición de la función.
debe pertenecer al dominio de definición de la función.
Composición de funciones
Si tenemos dos funciones:  y
y  , de modo que el dominio de la
, de modo que el dominio de la 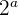 esté incluido en el recorrido de la
esté incluido en el recorrido de la 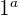 , se puede definir una nueva función que asocie a cada elemento del dominio de
, se puede definir una nueva función que asocie a cada elemento del dominio de  el valor de
el valor de  .
.
Función inversa o recíproca
Se llama función inversa o reciproca de  a otra función
a otra función  que cumple que:
que cumple que:
Si  , entonces
, entonces  .
.
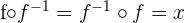
Cálculo de la función inversa
1 Se escribe la ecuación de la función en  e
e  .
.
2 Se intercambian las variables.
3 Se despeja la variable  en función de la variable
en función de la variable  .
.
Crecimiento y decrecimiento
Tasa de variación
El incremento de una función se llama tasa de variación, y mide el cambio de la función al pasar de un punto a otro.

Función estrictamente creciente
 es estrictamente creciente en a si sólo si existe un entorno de
es estrictamente creciente en a si sólo si existe un entorno de  , tal que para toda
, tal que para toda  que pertenezca la entorno de
que pertenezca la entorno de  se cumple:
se cumple:


La tasa de variación es positiva.
Función creciente
 es creciente en a si sólo si existe un entorno de
es creciente en a si sólo si existe un entorno de  , tal que para toda
, tal que para toda  que pertenezca la entorno de
que pertenezca la entorno de  se cumple:
se cumple:
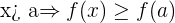
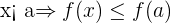
La tasa de variación es positiva o igual a cero.
Función estrictamente decreciente
 es estrictamente decreciente en
es estrictamente decreciente en  si sólo si existe un entorno de
si sólo si existe un entorno de  , tal que para toda
, tal que para toda  que pertenezca la entorno de a se cumple:
que pertenezca la entorno de a se cumple:
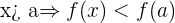

La tasa de variación es negativa.
Función decreciente
 es decreciente en
es decreciente en  si sólo si existe un entorno de
si sólo si existe un entorno de  , tal que para toda
, tal que para toda  que pertenezca la entorno de a se cumple:
que pertenezca la entorno de a se cumple:


La tasa de variación es negativa o igual a cero.
Cotas
Función acotada superiormente
Una función  está acotada superiormente si existe un número real
está acotada superiormente si existe un número real  tal que para toda
tal que para toda  es
es  .
.
El número  se llama cota superior.
se llama cota superior.
Función acotada inferiormente
Una función  está acotada inferiormente si existe un número real
está acotada inferiormente si existe un número real 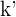 tal que para toda
tal que para toda  es
es  .
.
El número 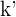 se llama cota inferior.
se llama cota inferior.
Función acotada
Una función esta acotada si lo está a superior e inferiormente.
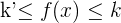
Máximo absoluto
Una función tiene su máximo absoluto en el  si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.
si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.
Mínimo absoluto
Una función tiene su mínimo absoluto en el 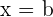 si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
Máximo y mínimo relativo
Una función  tiene un máximo relativo en el punto a si
tiene un máximo relativo en el punto a si  es mayor o igual que los puntos próximos al punto
es mayor o igual que los puntos próximos al punto  .
.
Una función  tiene un mínimo relativo en el punto
tiene un mínimo relativo en el punto  si
si  es menor o igual que los puntos próximos al punto
es menor o igual que los puntos próximos al punto  .
.
Simetría
Una función  es simétrica respecto del eje de ordenadas cuando para todo
es simétrica respecto del eje de ordenadas cuando para todo  del dominio se verifica:
del dominio se verifica:

Las funciones simétricas respecto del eje de ordenadas reciben el nombre de funciones pares.
Simetría respecto al origen
Una función  es simétrica respecto al origen cuando para todo
es simétrica respecto al origen cuando para todo  del dominio se verifica:
del dominio se verifica:

Las funciones simétricas respecto al origen reciben el nombre de funciones impares.
Funciones periódicas
Una función  es periódica, de período
es periódica, de período  , si para todo número entero
, si para todo número entero  , se verifica:
, se verifica:
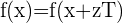
Si tenenos una función periódica  de periodo
de periodo  , la función
, la función  tiene de periodo:
tiene de periodo:
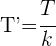














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Está mal la solución de la función inversa de f(x) = (2x+3)/x-1
Ya lo revise y no encuentro el error, podrías señalar en que está mal.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis