Temas

Área bajo la curva de una función que toma valores positivos
Si la función toma valores positivos en un intervalo 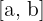 entonces la gráfica de la función está por encima del eje de abscisas. El área de la función viene dada por:
entonces la gráfica de la función está por encima del eje de abscisas. El área de la función viene dada por:
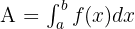
Para hallar el área seguiremos los siguientes pasos:
1 Se calculan los puntos de corte con con el eje  , haciendo
, haciendo  y resolviendo la ecuación.
y resolviendo la ecuación.
2 El área es igual a la integral definida de la función que tiene como límites de integración los puntos de corte.
Ejemplos de áreas limitadas por funciones positivas
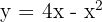 y el eje
y el eje 
En primer lugar hallamos los puntos de corte con el eje  para representar la curva y conocer los límites de integración, es decir, igualamos la función a cero y las resolvemos.
para representar la curva y conocer los límites de integración, es decir, igualamos la función a cero y las resolvemos.
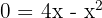
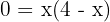
 y
y 

Calculamos la integral:
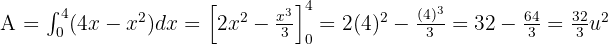
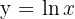 entre el punto de corte con el eje
entre el punto de corte con el eje  y el punto de abscisa
y el punto de abscisa  .
. 
Aplicando la exponencial de ambos lados
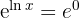

ya que 
finalmente el punto de corte es 

Ahora vamos a encontrar el área bajo la curva por medio de la siguiente integral, por el método de integración por partes, es decir, 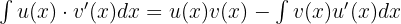 :
:

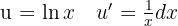

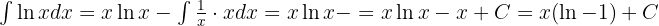
Entonces,
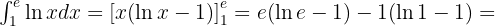
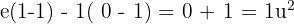
Área bajo la curva de una función que toma valores negativos
Si la función toma valores negativos en un intervalo 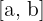 entonces la gráfica de la función está por debajo del eje de abscisas. El área de la función viene dada por un viene dada por:
entonces la gráfica de la función está por debajo del eje de abscisas. El área de la función viene dada por un viene dada por:

Ejemplos de áreas limitadas por funciones negativas
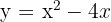 y el eje
y el eje 
En primer lugar hallamos los puntos de corte con el eje  para representar la curva y conocer los límites de integración, es decir, igualamos la función a cero y las resolvemos.
para representar la curva y conocer los límites de integración, es decir, igualamos la función a cero y las resolvemos.

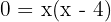
 y
y 
Calculamos la integral:
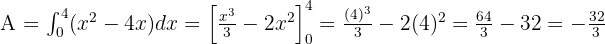
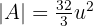
 y el eje
y el eje  entre
entre  y
y  .
.

Resolvemos la integral:
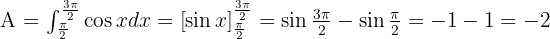

Área de una función que toma valores positivos y negativos

En ese caso el área tiene zonas por encima y por debajo del eje de abscisas. Para calcular el área de la función seguiremos los siguientes pasos:
1 Se calculan los puntos de corte con con el eje  , haciendo
, haciendo  y resolviendo la ecuación.
y resolviendo la ecuación.
2 Se ordenan de menor a mayor las raíces, que serán los límites de integración.
3 El área es igual a la suma de las integrales definidas en valor absoluto de cada intervalo.
Ejemplo
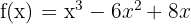 y el eje
y el eje  .
.  para representar la curva y conocer los límites de integración, es decir, igualamos la función a cero y las resolvemos.
para representar la curva y conocer los límites de integración, es decir, igualamos la función a cero y las resolvemos. 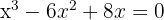


 y
y 
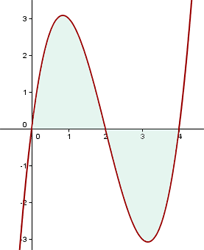
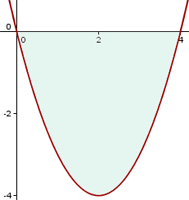
Observando la gráfica tenemos que calcular dos integrales una para la función que toma valores positivos en el intervalo  y otra para la función que toma valores negativos en el intervalo
y otra para la función que toma valores negativos en el intervalo  .
.

La gráfica es simétrica, por lo tanto el área se puede escribir como:
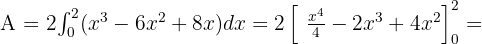
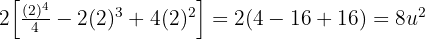
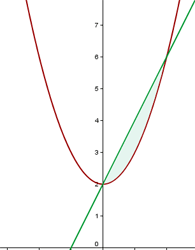
Área comprendida entre dos funciones
El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo.
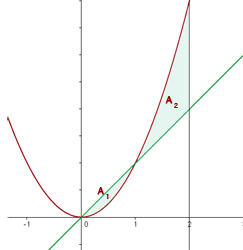
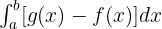
Calcular el área del círculo de radio r
Partimos de la ecuación de la circunferencia 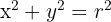 .
.
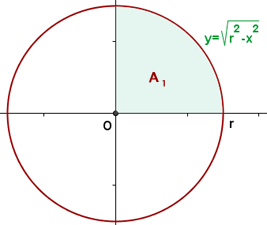
El área del círculo es cuatro veces el área del primer cuadrante.
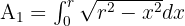
Calculamos la integral indefinida por cambio de variable:
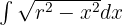

Entonces,
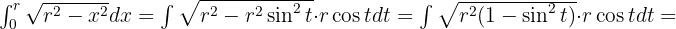

Hallamos los nuevos límites de integración.


Finalmente,

Cómo la gráfica es simétrica:














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en el ejercicio 26 el resultado no se ve bien, como quedaria?
Disculpa pero no hay ejercicio 26, solo llega al 20.
estan la mitad de los ejercicios incorrectos, revisarlos por favor
Podrías indicarnos que ejercicios están mal, pues ya revise y no encontre los errores.
En el ejercicio 13 que es la integral de x^2 * ln(x^2), al hacerlo por partes hace bien lo de coger como u=ln(x^2), pero al coger x^2 como v’ se equivoca y lo coge como x^3
Una disculpa ya se corrigió.
hola me ayudas con este ejercicio
Dada la región R cerrada del plano, limitada por las curvas:
y=x^2, x+y=6, x=4, y=0
a) Represente gráficamente la región R
Utilice el cálculo integral para determinar:
b)El área de la región R. (utilice integrales dobles)
c)El volumen del sólido de revolución que se obtiene al girar la región R
alrededor del eje X
d)La coordenada del centroide de la placa delgada determinada por la región
R, si se conoce que tiene densidad constante.
En la pagina no deja ver las respuestas, me parece que es un error de vosotros a ver si lo podeis arreglar, mil gracias
Hola, Pancracio:
Las soluciones ya aparecen correctamente 🙂
Un saludo
Estudio carrera de ingeniería pero me cuesta mucho las matemáticas ¿ algún consejo? O tips