Temas
En este artículo introduciremos formalmente qué es una sucesión y mencionaremos definiciones importantes relacionadas con éstas.

Introducción
Una sucesión es un conjunto de elementos, comúnmente números, dispuestos uno a continuación de otro
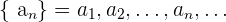
A cada elemento dentro de la sucesión se le conoce como término de la sucesión. El subíndice indica el lugar que el término ocupa en la sucesión.Así, en general,  denota al n-ésimo término de la sucesión
denota al n-ésimo término de la sucesión 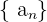 . Por ejemplo, el décimo término de la sucesión
. Por ejemplo, el décimo término de la sucesión 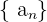 es
es 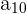 .
.
Determinación de una sucesión
Término general
Podemos determinar una sucesión por medio de lo que conocemos término general. El término general nos ayuda a calcular el valor de cada término de la sucesión con base a su posición. En general, tenemos que
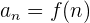
y denotamos como

Ejemplo: Encontrar los primeros cinco términos de la sucesión 
La sucesión está dada por el término general 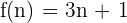
Para encontrar los términos de la sucesión, sustituimos los valores de 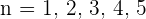
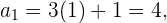
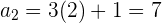
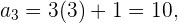


Formalmente las sucesiones se conocen como funciones que van del conjunto de los números naturales al conjunto de los números reales, esto es
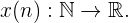
Por recurrencia
Aunque la recurrencia no es muy formal es común ver sucesiones definidas por este método. La recurrencia consiste en definir un número finitos de términos por un valor específico y los demás por medio de operaciones entre los términos anteriores, estas operaciones las definimos por medio de una función de la forma
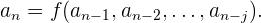
Comúnmente sólo definimos el primer término con un valor específico y los demás términos como una función del término anterior inmediato.
Ejemplo: Encontrar los primeros cinco términos de la sucesión 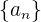 definida por
definida por 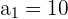 y
y  para
para  .
.
Los términos de la sucesión vienen definidos a partir del término anterior, esto es, a partir conocer un término podemos encontra el término siguiente. Conocemos el primer término 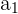 , entonces podemos encontrar el segundo término
, entonces podemos encontrar el segundo término 

Conocemos el segundo término  , entonces podemos encontrar el tercer término
, entonces podemos encontrar el tercer término 
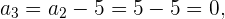
Conocemos el tercer término  , entonces podemos encontrar el cuarto término
, entonces podemos encontrar el cuarto término 
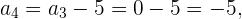
Conocemos el cuarto término  , entonces podemos encontrar el quinto término
, entonces podemos encontrar el quinto término 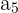

dando como resultado
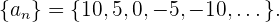
Operaciones entre sucesiones
Es esta parte veremos las operaciones que se pueden hacer entre sucesiones o bien entre una sucesión y un número real.
Suma de sucesiones
Si tenemos dos sucesiones  y
y  , la suma de estas sucesiones es una nueva sucesión
, la suma de estas sucesiones es una nueva sucesión 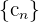

en pocas palabras, sumamos los términos que están en la misma posición.
Ejemplo: Encuentra la suma de las siguientes sucesiones
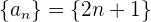
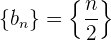
Calculamos los términos de cada sucesión
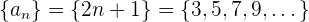

Sumando término a término se obtiene
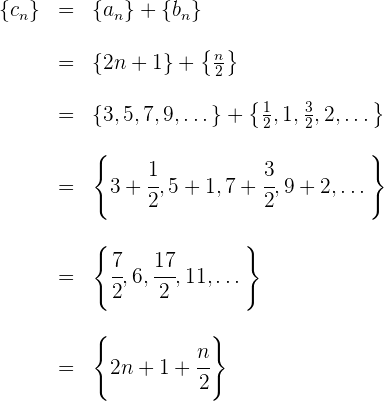
Notemos que el término general de la suma es igual a la suma de los términos generales de las sucesiones involucradas.
Propiedades de la suma de sucesiones
1 Conmutatividad: Si tenemos dos sucesiones  y
y  , entonces se cumple que
, entonces se cumple que

2 Asociatividad: Si tenemos tres sucesiones  ,
,  y
y 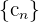 , entonces se cumple que
, entonces se cumple que
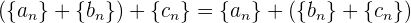
3 Elemento neutro: Existe la sucesión 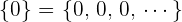 tal que
tal que
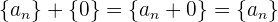
4 Elemento inverso: Para toda sucesión  existe la sucesión
existe la sucesión 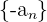 , la cual tiene los mismo elementos que
, la cual tiene los mismo elementos que  pero con signo opuesto, tal que
pero con signo opuesto, tal que
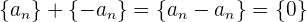
Resta de sucesiones
Si tenemos dos sucesiones  y
y  , la resta
, la resta 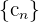 de estas sucesiones se define como
de estas sucesiones se define como
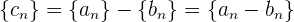
en pocas palabras, restamos los términos que están en la misma posición.
Ejemplo: Encuentra la resta de las siguientes sucesiones
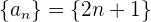
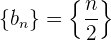
Calculamos los términos de cada sucesión
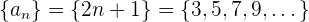

Restando término a término se obtiene
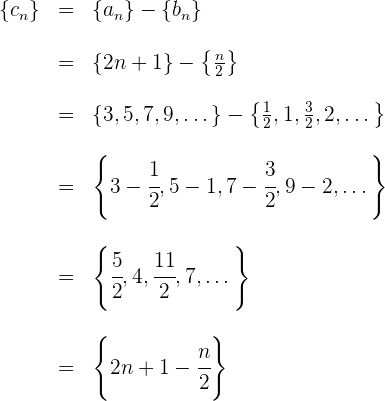
Notemos que el término general de la resta es igual a la resta de los términos generales de las sucesiones involucradas.
La resta de  y
y  es equivalente a la suma de
es equivalente a la suma de  y
y  , en donde
, en donde  es el inverso de
es el inverso de  respecto a la suma.
respecto a la suma.
Multiplicación de sucesiones
Si tenemos dos sucesiones  y
y  , la multiplicación de estas sucesiones se define como
, la multiplicación de estas sucesiones se define como
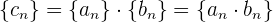
en pocas palabras, multiplicamos los términos que están en la misma posición.
Ejemplo: Encuentra la multiplicación de las siguientes sucesiones


Calculamos los términos de cada sucesión
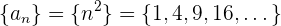

Multiplicando término a término se obtiene

Notemos que el término general de la multiplicación es igual a la multiplicación de los términos generales de las sucesiones involucradas.
Propiedades de la multiplicación de sucesiones
1 Conmutatividad: Si tenemos dos sucesiones  y
y  , entonces se cumple que
, entonces se cumple que
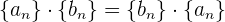
2 Asociatividad: Si tenemos tres sucesiones  ,
,  y
y 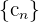 , entonces se cumple que
, entonces se cumple que
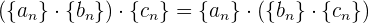
3 Elemento neutro: Existe la sucesión 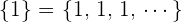 tal que
tal que
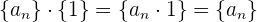
4 Elemento inverso: Para toda sucesión  , tal que
, tal que 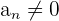 para todo
para todo  , existe la sucesión
, existe la sucesión  , la cual tiene los recíprocos de los elemetos de
, la cual tiene los recíprocos de los elemetos de  y cumple que
y cumple que
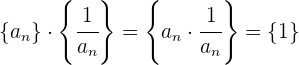
5 Distributividad respecto a la suma: Si tenemos tres sucesiones  ,
,  y
y 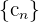 , entonces se cumple que
, entonces se cumple que

Si vives en la capital, seguro que te interesan nuestras clases particulares matematicas madrid.
División de sucesiones
Si tenemos dos sucesiones  y
y  , la divisón de estas sucesiones se define como
, la divisón de estas sucesiones se define como

en pocas palabras, dividimos los términos que están en la misma posición. Notemos que todos los términos de  deben de ser distintos de cero, esto porque la división entre cero no está bien definida.
deben de ser distintos de cero, esto porque la división entre cero no está bien definida.
Ejemplo: Encuentra la división de 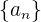 entre
entre 


Calculamos los términos de cada sucesión
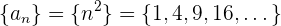

Dividiendo término a término se obtiene
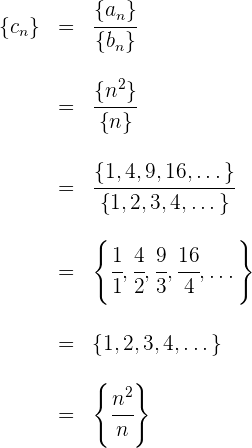
Notemos que el término general de la división es igual a la división de los términos generales de las sucesiones involucradas.
La división de  y
y  es equivalente a la multiplicación de
es equivalente a la multiplicación de  y
y 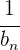 , en donde
, en donde  es el inverso de
es el inverso de  respecto a la multiplicación.
respecto a la multiplicación.
Límite de una sucesión
Dada una sucesión  , decimos que el límite de esta es el valor al cual se van acercandos los elementos de la sucesión conforme
, decimos que el límite de esta es el valor al cual se van acercandos los elementos de la sucesión conforme  crece. Comúnmente el límite se denota por
crece. Comúnmente el límite se denota por  .
.
Ejemplo: Encuentra el límite de la sucesión
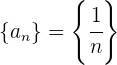
Lo términos de la sucesión son:
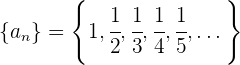
Hay que notar que conforme  crece, el término
crece, el término  se hace más pequeño.
se hace más pequeño.
La sucesión tiene como límite 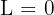 , esto ya que conforme
, esto ya que conforme  crece
crece  se acerca al cero.
se acerca al cero.
Ahora bien, no todas las sucesiones tienen límite, en este caso se tienen tres posibilidades:
1 Convergente. Una sucesión  se dice que converge si tiene límite.
se dice que converge si tiene límite.
2 No convergente. Una sucesión  se dice que no converge si no tiene límite.
se dice que no converge si no tiene límite.
3 Divergente. Una sucesión  se dice que diverge a infinito o menos infinito si sus términos se van aproximando a infinito (
se dice que diverge a infinito o menos infinito si sus términos se van aproximando a infinito ( ) o a menos infinito (
) o a menos infinito ( ), respectivamente, conforme
), respectivamente, conforme  crece.
crece.
Ejemplos: La sucesión
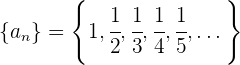
es convergente ya que 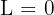 .
.
La sucesión
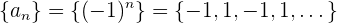
no tiene límite ya que sus elementos se van alternando entre  y
y  , por lo cual no es convergente.
, por lo cual no es convergente.
La sucesión
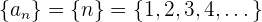
es divergente ya que sus términos siguen y siguen creciendo sin parar conforme  crece.
crece.
Sucesiones monótonas
En esta parte clasificaremos las sucesiones respecto a la forma en que comparamos cada par consecutivo de términos.
Sucesión monótona creciente
Una sucesión  es monótona creciente (o monótonamente creciente) si para cada par de términos consecutivos
es monótona creciente (o monótonamente creciente) si para cada par de términos consecutivos  y
y 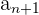 se cumple que
se cumple que
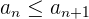
Ejemplo: Para la sucesión

notamos que
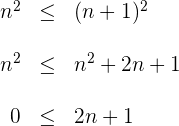
La última inecuación se cumple para todo  , por lo tanto la sucesión es monónona creciente.
, por lo tanto la sucesión es monónona creciente.
Sucesión estrictamente creciente
Una sucesión  es estrictamente creciente si para cada par de términos consecutivos
es estrictamente creciente si para cada par de términos consecutivos  y
y 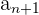 se cumple que
se cumple que
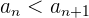
Ejemplo: Para la sucesión
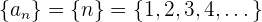
notamos que

La última inecuación se cumple siempre, por lo tanto la sucesión es estrictamente creciente.
Sucesión monótona decreciente
Una sucesión  es monótona decreciente (o monótonamente decreciente) si para cada par de términos consecutivos
es monótona decreciente (o monótonamente decreciente) si para cada par de términos consecutivos  y
y 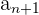 se cumple que
se cumple que
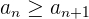
Ejemplo: Para la sucesión

notamos que
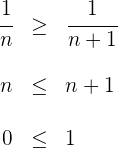
La última inecuación se cumple para todo  , por lo tanto la sucesión es monónona decreciente.
, por lo tanto la sucesión es monónona decreciente.
Sucesión estrictamente decreciente
Una sucesión  es estrictamente decreciente si para cada par de términos consecutivos
es estrictamente decreciente si para cada par de términos consecutivos  y
y 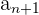 se cumple que
se cumple que

Ejemplo: Para la sucesión
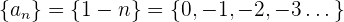
notamos que
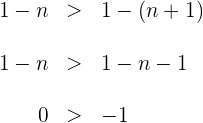
La última inecuación se cumple siempre, por lo tanto la sucesión es estrictamente decreciente.
Sucesiones acotadas
Aquí veremos lo que es una sucesión acotada y los distintos tipos de cotas.
Sucesión acotada inferiomente
Una sucesión  está acotada inferiormente si existe un número real
está acotada inferiormente si existe un número real  tal que
tal que

en pocas palabras, si 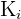 es menor o igual que todos los términos de la sucesión. En este caso decimos que
es menor o igual que todos los términos de la sucesión. En este caso decimos que 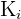 es una cota inferior de
es una cota inferior de  . Notemos que todo número real
. Notemos que todo número real  que cumpla que
que cumpla que

es una cota inferior de  .
.
Ejemplo: Para la sucesión
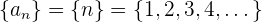
siempre se cumple que
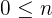
Así tenemos que  es una cota inferior de
es una cota inferior de  . Por lo tanto
. Por lo tanto  es una sucesión acotada inferiormente. Igual los números
es una sucesión acotada inferiormente. Igual los números  ,
,  también son cotas inferiores de
también son cotas inferiores de  .
.
Sucesión acotada superiormente
Una sucesión  está acotada superiormente si existe un número real
está acotada superiormente si existe un número real  tal que
tal que

en pocas palabras, si 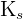 es mayor o igual que todos los términos de la sucesión. En este caso decimos que
es mayor o igual que todos los términos de la sucesión. En este caso decimos que 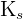 es una cota superior de
es una cota superior de  . Notemos que todo número real
. Notemos que todo número real  que cumpla que
que cumpla que

es una cota superior de  .
.
Ejemplo: Para la sucesión

siempre se cumple que
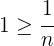
Así tenemos que  es una cota superior de
es una cota superior de  . Por lo tanto
. Por lo tanto  es una sucesión acotada superiormente. Igual los números
es una sucesión acotada superiormente. Igual los números  ,
,  también son cotas superiores de
también son cotas superiores de  .
.
Sucesión totalmente acotada
Una sucesión  está totalmente acotada si está acotada inferior y superiormente. En otras palabras, si existen números reales
está totalmente acotada si está acotada inferior y superiormente. En otras palabras, si existen números reales 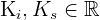 tales que
tales que

¿Necesitas clases particulares matematicas?
Otra definición equivalente es que  está totalmente acotada si existe número real
está totalmente acotada si existe número real  tal que
tal que
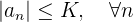
Ejemplo: Para la sucesión que analizamos previamente

siempre se cumple que
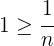
Así tenemos que  es una cota superior de
es una cota superior de  .
.
Además, 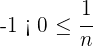 para toda
para toda  , por lo tanto
, por lo tanto

Así tenemos que 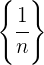 es una sucesión totalmente acotada.
es una sucesión totalmente acotada.
Progresiones Aritméticas
Una progresión aritmética es una sucesión de números donde cada término  es igual a un número fijo
es igual a un número fijo  más
más  veces una cantidad
veces una cantidad  (llamada diferencia). La fórmula está dada por
(llamada diferencia). La fórmula está dada por
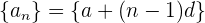
o bien

Notemos que esta sucesión está completamente definida por  y
y  . Además la fórmula es muy parecida a la de una recta
. Además la fórmula es muy parecida a la de una recta 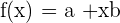 en donde nuestros valores de
en donde nuestros valores de  tomarían solo números naturales.
tomarían solo números naturales.
Notemos que en una sucesión aritmética siempre tenemos que

por este motivo se suele decir que una sucesión aritmética tiene la forma
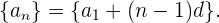
Ejemplo: Encontrar los términos de la sucesión aritmética

Notamos que  y
y 
Evaluamos el término general para los distintos valores de 

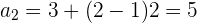
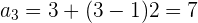

Observa que dos términos consecutivos difieren en 
Progresiones geométricas
Una progresión geométrica es una sucesión de números donde cada término  es igual a un número fijo
es igual a un número fijo  multilpicado por una cantidad
multilpicado por una cantidad  (llamada razón) elevada a la potencia
(llamada razón) elevada a la potencia  . La fórmula está dada por
. La fórmula está dada por
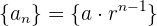
Notemos que esta sucesión está completamente definida por  y
y  .
.
Notemos que en una sucesión geométrica siempre tenemos que
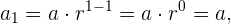
por este motivo se suele decir que una sucesión geométrica tiene la forma

Ejemplo: Encuentra los términos de la sucesión geométrica
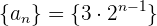
Notamos que 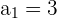 y
y 
Evaluamos el término general para los distintos valores de 
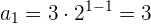
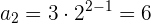

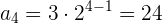
Término general de una sucesión
Para poder obtener el término general aquí te dejamos algunas recomendaciones
1 Comprobar si es una progresión aritmética.
2 Comprobar si es una progresión geométrica.
3 Comprobar si los términos son cuadrados perfectos.
4 Si los términos de la sucesión cambian de signo de forma alternada. En estos casos suele haber un término  (pares positivos) o
(pares positivos) o 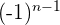 (impares positivos) multiplicando los término, haciendo que estos alternen.
(impares positivos) multiplicando los término, haciendo que estos alternen.
5 Si los términos de la sucesión son fraccionarios (no siendo una progresión), entonces se calcula el término general del numerador y denominador por separado.
Ejemplo: Encontrar el término general de la sucesión
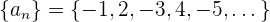
Observamos que en valor absoluto los términos son consecutivos.
El signo del primer término es negativo y luego estos se van alternando. Así, el término general viene dado por

Ejemplo: Encontrar el término general de la sucesión
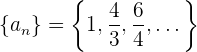
Observamos que el numerador del segundo y tercer término son pares consecutivos por lo que proponemos 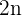 .
.
De la misma forma el denominador del segundo y tercer término son enteros consecutivos por lo que proponemos  .
.
El término general propuesto es 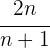 .
.
Verificamos que el término general propuesto satisface el primer término
 .
.
Como los términos proporcionados satisfacen la expresión propuesta, concluimos que














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma.de los 9 primeros términos de una progresión es 219, si el primer término de la progresión es -4, habllar el último término An.
Son todos los tiempos de sucesiones?
No es clara tu pregunta, si te refieres a los ejercicios de inversión y depende del problema planteado.
Tres números x y z forman una progresión geométrica creciente que cumple x + y + z = 21 y x por y por z = 2 16 determina la razón de la progresión dada
Cuál es el número de término de una progresión aritmética cuando la diferencia común de los términos en 5,el primer término es 1 y el último es 46
En una PG a9 =56yr =1 , hallar a6
2
Encuentra el 6to,8vo,10mo termino de la siguiente sucesión geometrica3,6,12,14
Una progresión geométrica de razón positiva consta de 4 terminos
Porfa alguien me puede ayudar a comprender como puedo resolver un ejercisio sobre Sumar todos los términos de la progresión
1,34, 916, 2764, … y ando mas perdidaa