Al tratar de resolver un sistema de ecuaciones uno se puede encontrar con que hay muchas formas diferentes de hacerlo como el método de Gauss, regla de Cramer o el teorema Rouche-Frobenius.
Esto podría generar la pregunta: ¿Cuál método es el mejor?
A continuación haremos una comparación entre estos métodos resolviendo diferentes sistemas de ecuaciones y discutiremos sobre las ventajas y desventajas de usar cada uno de los métodos mencionados.

Sistemas homogéneos
Si un sistema de  ecuaciones y
ecuaciones y  incógnitas tiene todos los términos independientes nulos se dice que es homogéneo.
incógnitas tiene todos los términos independientes nulos se dice que es homogéneo.
Admiten la solución trivial:

La condición necesaria y suficiente para que un sistema homogéneo tenga soluciones distintas de la trivial es que el rango de la matriz de los coeficientes sea menor que el nº de incógnitas, o dicho de otra forma, que el determinante de la matriz de los coeficientes sea nulo.
Esto solo nos dice que el sistema tiene una solución diferente de la trivial, pero claramente no nos dice cual es. Por lo que para calcularla podemos hacer uso de los métodos mencionados.
Ejemplo
Resolver el siguiente sistema de ecuaciones:
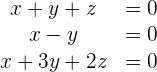
Solución con el método de Gauss-Jordan
1Formar una matriz de los coeficientes y los términos independientes.
Lo primero que tenemos que hacer es formar una matriz con los coeficientes y los términos independientes (números del lado derecho del signo de igualdad de las ecuaciones) de las ecuaciones de la siguiente manera:
 ,

2Usar un poco de álgebra para hacer la eliminación gaussiana.
Ahora procedemos a hacer las operaciones para encontrar la solución del sistema, por lo que hacemos:
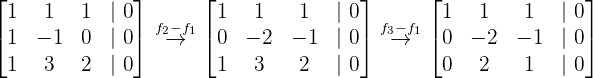


De esto obtenemos las ecuciones:
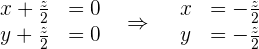
3Reescribir las variables.
En este caso tomamos  , tenemos que:
, tenemos que:  y
y  .
.
Esto para tener todas las variables en términos de una sola.
Lo que indica que el sistema tiene infinitas soluciones.
Solución con la regla de Cramer
1Formar la matriz de los coeficientes y calcular el determinante.
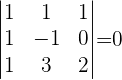
2Debido a que el determinante de la matriz de los coeficientes es  , no podemos hacer uso de la regla de cramer. Esto puede indicar que el sistema no tiene solución o tiene infinitas soluciones.
, no podemos hacer uso de la regla de cramer. Esto puede indicar que el sistema no tiene solución o tiene infinitas soluciones.
Solución con el teorema Rouche-Frobenius
1Formar la matriz de los coeficientes.
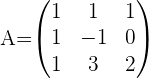
2Calcular el rango de la matriz de los coeficientes.
En este caso el rango de la matriz es:

3Formar la matriz ampliada.
Ahora agregamos los términos independientes del sistema de ecuaciones (números del lado derecho del signo de igualdad de las ecuaciones) a la matriz, por lo que formamos la matriz ampliada:
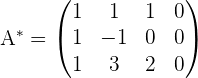
4Calcular el rango de la matriz ampliada.
En este caso el rango de la matriz ampliada es:
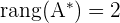
5Aplicamos el teorema de Rouché.
 Sistema Compatible.
Sistema Compatible. 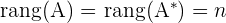 Sistema Compatible Determinado.
Sistema Compatible Determinado. Sistema Compatible Indeterminado.
Sistema Compatible Indeterminado.
 Sistema Incompatible.
Sistema Incompatible.
Donde  representa el número de variables.
representa el número de variables.
Como los rangos de ambas matrices coinciden, entonces el sistema es compatible, y además ya que el rango es menor al número de incógnitas entonces el sistema es compatible indeterminado, lo que indica que tiene infinitas soluciones.
Sistemas no homogéneos
¿Necesitas un profesor de mates?
Se dice que un sistema de ecuaciones es no homogéneo, cuando cada una de las ecuaciones involucradas en el sistema están igualadas a un número diferente de cero.
Ejemplo
Resolver el siguiente sistema de ecuaciones:
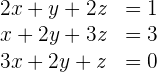
Solución con el método de Gauss-Jordan
1Formar la matriz de los coeficientes y los términos independientes.
Lo primero que tenemos que hacer es formar una matriz con los coeficientes y los términos independientes (números del lado derecho del signo de igualdad de las ecuaciones) de las ecuaciones de la siguiente manera:
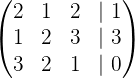
2Usar un poco de álgebra para hacer la eliminación gaussiana.
Antes de comenzar con a realizar las operaciones, cambiaremos la posición de las filas de la matriz de la siguiente manera para facilitar la resolución.

 
Ahora procedemos a hacer las operaciones para encontrar la solución del sistema, por lo que hacemos:

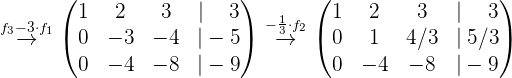

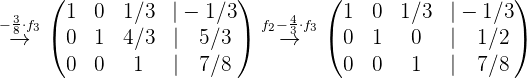
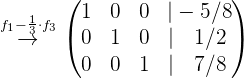
Lo que nos indica que la solución del sistema es:

Solución con la regla de Cramer
1Formar la matriz de los coeficientes y calcular el determinante.
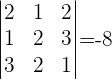
2Como el determinante es distinto de 0, la matriz es regular y el sistema tiene una única solución (sistema compatible determinado).
3Continuar con el procedimiento para resolver el sistema.
Ahora reemplazamos la primera columna de la matriz de los coeficientes por una columna formada por los términos independientes (números del lado derecho del signo de igualdad de las ecuaciones) y calculamos el determinante.
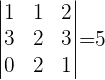
Ahora el valor de la variable  esta dado por:
esta dado por:
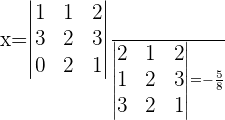
Si hacemos algo similar a esto podemos encontrar el valor de las variables restantes, cambiando la segunda columna de la matriz de coeficientes por la columna de los términos independientes y calculando su determinante, encontramos el valor de  de forma similar al de
de forma similar al de  , esto es lo mismo para la variable
, esto es lo mismo para la variable  pero cambiando la tercera columna. Si hacemos los cálculos obtenemos que:
pero cambiando la tercera columna. Si hacemos los cálculos obtenemos que:

Solución con el teorema Rouche-Frobenius
1Formar la matriz de los coeficientes
 
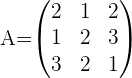
2Calcular el rango de la matriz de los coeficientes.
En este caso el rango de la matriz es:
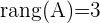
3Formar la matriz ampliada.
Ahora agregamos los términos independientes del sistema de ecuaciones (números del lado derecho del signo de igualdad de las ecuaciones) a la matriz, por lo que formamos la matriz ampliada:
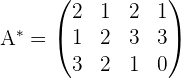
4Calcular el rango de la matriz ampliada.
En este caso el rango de la matriz ampliada es:
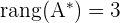
5Aplicamos el teorema de Rouché.
 Sistema Compatible.
Sistema Compatible. 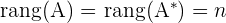 Sistema Compatible Determinado.
Sistema Compatible Determinado. Sistema Compatible Indeterminado.
Sistema Compatible Indeterminado.
 Sistema Incompatible.
Sistema Incompatible.
Donde  representa el número de variables.
representa el número de variables.
Como los rangos de ambas matrices coinciden, entonces el sistema es compatible, y además ya que el rango es igual al número de incógnitas entonces el sistema es compatible determinado, lo que indica que tiene una única solución.
Sistemas de ecuaciones con parámetros
En esta sección revisaremos como resolver sistemas de ecuaciones con parámetros con los métodos que hemos visto hasta ahora.
Ejemplo
Resolver el siguiente sistema de ecuaciones:
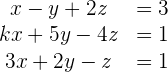
Solución con el método de Gauss-Jordan
1Formar una matriz de los coeficientes y los términos independientes.
Lo primero que tenemos que hacer es formar una matriz con los coeficientes y los términos independientes (números del lado derecho del signo de igualdad de las ecuaciones) de las ecuaciones de la siguiente manera:
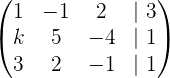
2Usar un poco de álgebra para hacer la eliminación gaussiana.
Ahora procedemos a hacer las operaciones para encontrar la solución del sistema
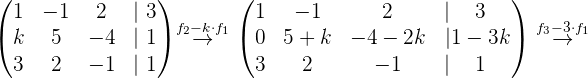


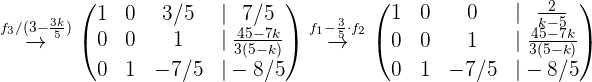
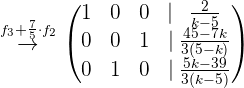
Rápidamente notamos que si  , entonces no existirían la solución del sistema de ecuaciones. Por lo que suponemos que
, entonces no existirían la solución del sistema de ecuaciones. Por lo que suponemos que 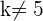 .
.
Por lo que tenemos que la solución del sistema es:

Solución con la regla de Cramer
1Formar la matriz de los coeficientes y calcular el determinante.
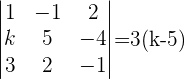
2Notamos que si  entonces el determinante es
entonces el determinante es  y significaría que no podemos utilizar la regla de Cramer. Por lo que vamos a suponer que
y significaría que no podemos utilizar la regla de Cramer. Por lo que vamos a suponer que 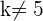 .
.
3Sustituimos la primera columna por columna de los términos independientes y calculamos el determinante.

4Sustituimos la segunda columna por columna de los términos independientes y calculamos el determinante.
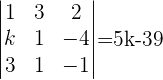
5Sustituimos la tercera columna por columna de los términos independientes y calculamos el determinante.
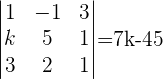
5Calculamos el valor de las variables  ,
,  y
y  .
.
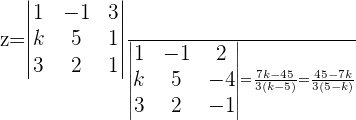
Por la regla de cramer sabemos que:
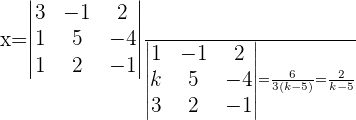
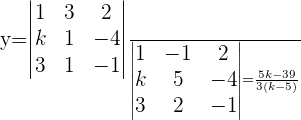
Solución con el teorema Rouche-Frobenius
1Formar la matriz de los coeficientes.
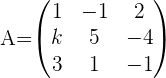
2Calcular el rango de la matriz de los coeficientes.
En este caso el rango de la matriz depende del determinante de la matriz el cual es:
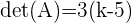
Notamos que si  entonces el determinante es
entonces el determinante es  , por lo que el rango de la matriz sería
, por lo que el rango de la matriz sería  .
.
Ahora si 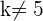 entonces el determinante es
entonces el determinante es 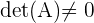 , por lo que el rango en este caso es
, por lo que el rango en este caso es 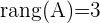
3Formar la matriz ampliada.
Ahora agregamos los términos independientes del sistema de ecuaciones (números del lado derecho del signo de igualdad de las ecuaciones) a la matriz, por lo que formamos la matriz ampliada:

4Calcular el rango de la matriz ampliada.
En este caso el rango de la matriz ampliada es:
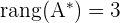
 Sistema Compatible.
Sistema Compatible. 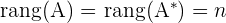 Sistema Compatible Determinado.
Sistema Compatible Determinado. Sistema Compatible Indeterminado.
Sistema Compatible Indeterminado.
 Sistema Incompatible.
Sistema Incompatible.
Donde  representa el número de variables.
representa el número de variables.
Si  , entonces el rango de las matrices es diferente, por lo que tenemos un sistema incompatible.
, entonces el rango de las matrices es diferente, por lo que tenemos un sistema incompatible.
Si 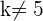 entonces los rangos de ambas matrices coinciden, entonces el sistema es compatible, y además ya que el rango es igual al número de incógnitas entonces el sistema es compatible determinado, lo que indica que tiene una única solución.
entonces los rangos de ambas matrices coinciden, entonces el sistema es compatible, y además ya que el rango es igual al número de incógnitas entonces el sistema es compatible determinado, lo que indica que tiene una única solución.
| Método de solución. | Ventajas | desventajas |
|---|---|---|
| Método de Gauss-Jordan | Es un método simple, fácil de aprender y recordar, además con él podemos ver que forman tienen las soluciones de los sistemas compatibles indeterminados. | No podemos conocer el tipo de sistema que estamos resolviendo hasta llegar prácticamente al final de las operaciones. |
| Regla de Cramer | Con este método podemos saber si el sistema a resolver tiene una única solución o no con sólo calcular el determinante de la matriz de coeficientes. | Con este método solo podemos resolver sistemas compatibles determinados, y no podemos ver que forma tienen las soluciones de sistemas compatibles indeterminados, o si el sistema es incompatible. |
| Teorema Rouche-Frobenius | Con sólo calcular el rango de dos matrices (la matriz de coeficientes y la matriz ampliada) podemos saber que tipo de sistema estamos resolviendo (compatible indeterminado, compatible determinado, incompatible). | No podemos calcular las soluciones (en caso de que existan) solo usando este método, para encontrarlas debemos hacer uso de otros métodos (regla de Cramer y método Gauss-Jordan). |













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudaria con este ejercicio
Tarea1
———
El Ministerio del Poder Popular para el Ecosocialismo proporciona tres tipos
de comida para tres tipos de especies de aves que alberga el aviario del Zoo
Aquarium de Valencia.
i) Cada ave de la especie 1 consume cada semana un promedio de 1 kilo
de alimento 1, 1 kilo de alimento 2 y 2 kilos de alimento 3.
ii) Cada ave de la especie 2 consume cada semana un promedio de 5 kilos
de alimento 1, 6 kilos de alimento 2 y 9 kilos de alimento 3.
iii) Cada ave de la especie 3 consume cada semana un promedio de 3 kilos
de alimento 1, 2 kilos de alimento 2 y 7 kilos de alimento 3.
Cada semana se proporciona al Zoo 350 kilos de alimento 1, 300 kilos de
alimento 2 y 750 kilos del alimento 3. Si se supone que las aves se comen todo
el alimento. ¿ Cuantas aves de cada especie pueden coexistir en el aviario?
Y asi quedaria la ecuacion:
+ 1 x1 + 5 y2 + 3 z3 = + 350
+ 1 x1 + 6 y2 + 2 z3 = + 300
+ 2 x1 + 9 y2 + 7 z3 = + 750
Me ayudarian en este caso..
Gracias
Tres resmas de papel tienen un valor de 33900
Cual es el precio de una resma
Me pueden ayudar con el procedimiento
Es un ejercicio planteamiento con resolución de ecuaciones lineales
Ayudenme por favor
33900/3 = 11300
El valor de una resma de papel es de 11300
Ecuaciones Lineales método Gauss Joroan
2×1-6×2-×3=-38
-3×1-×2+7×3=-34
-8×1-×2-2×3=-20
Multiplica por 4 la primera ecuacion y despues sumala con la que esta abajo se eliminara la y despues despeja la x que queda y encuentra su valor por ultimo usa una de las ecuaciones y sustituye el valor k encontraste en x y despeja la y listo
Para solucionar este problema debes plantear en primer lugar, la ecuación, la cual es la siguiente:
3*X = 33900
Luego de esto deberás despejar X, la cual corresponde al precio de una sola resma de papel, para ello deberás, pasar 33900 correspondiente a el precio total de las resmas de papel a dividir en 3, correspondiente al numero de resmas de papel, cabe mencionar que el precio total de las resmas de papel se divide en 3, puesto que 33900 estaba multiplicando, y por lo tanto al pasarlo al otro lado del igual automáticamente modifica su operación, en este caso el contrario de la multiplicación es la división, quedando así:
X=33900/3
Luego de hacer su respectiva operación, obtenemos como resultado final:
X=11300
Concluyendo finalmente que el valor de una sola resma de papel por el método de resolución de ecuaciones lineales corresponde a 11300