Temas

Unidad imaginaria
Se llama así al número 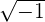 y se designa por la letra
y se designa por la letra 
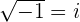
Las raíz cúbica de  no es un numero imaginario ni complejo.
no es un numero imaginario ni complejo.
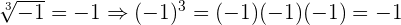
Ejemplos con unidad imaginaria
1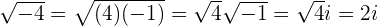
2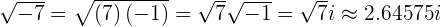
3
4 
¿Prefieres las clases matematicas online? Entonces, ¡pide ya la primera gratis en Superprof!
Número complejo
Al número 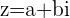 se le llama número complejo en forma binómica o binomial. En general, cualquier número complejo se denota por la letra
se le llama número complejo en forma binómica o binomial. En general, cualquier número complejo se denota por la letra  .
.
Al número  se llama parte real del número complejo y se denota por
se llama parte real del número complejo y se denota por  , mientras que al número
, mientras que al número  se llama parte imaginaria del número complejo y se denota por
se llama parte imaginaria del número complejo y se denota por  .
.
Si la parte imaginaria de un número complejo vale cero, esto es  , se reduce a un número real
, se reduce a un número real  , ya que
, ya que 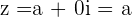 .
.
Si la parte real de un número complejo vale cero, esto es 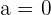 , el número complejo se reduce a
, el número complejo se reduce a  , y se dice que es un número imaginario puro.
, y se dice que es un número imaginario puro.
En general, al conjunto de todos números complejos se le designa por el símbolo 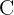 . De una manera más formal, utilizando notación de conjuntos, se le denota como:
. De una manera más formal, utilizando notación de conjuntos, se le denota como:
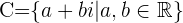
Los números complejos 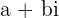 y
y 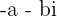 se llaman opuestos o contrarios.
se llaman opuestos o contrarios.
Los números complejos  y
y  se llaman complejos conjugados.
se llaman complejos conjugados.
Dos números complejos son iguales cuando tienen la misma componente real y la misma componente imaginaria, es decir:

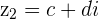
con  o
o 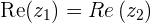 y
y  o
o 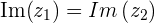
¿Buscas una profesora de matematicas? No se diga más: ¡encuéntrala en Superprof!
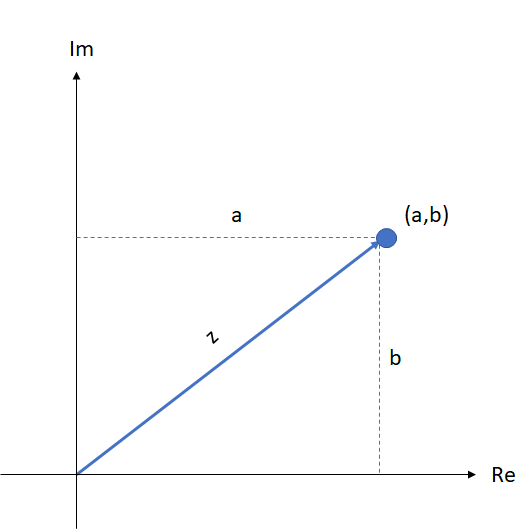
Representación gráfica de los números complejos
Los números complejos se representan gráficamente en el plano cartesiano (que en este caso de va a llamar plano complejo,  por sus iniciales) en forma de vector posicional, es decir, un vector cuyo punto inicial es el origen y su punto final el punto
por sus iniciales) en forma de vector posicional, es decir, un vector cuyo punto inicial es el origen y su punto final el punto  , también llamado afijo del número complejo. El eje
, también llamado afijo del número complejo. El eje  se llama eje real y el eje
se llama eje real y el eje  , eje imaginario.
, eje imaginario.
Al plano complejo también se le conoce como plano de Argand.
Potencias de la unidad imaginaria

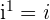
 , ya que
, ya que 
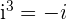 , ya que
, ya que 
 , ya que
, ya que  o
o 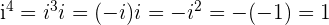
Ejemplos de potencias superiores de números complejos
1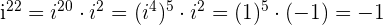
2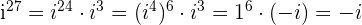
3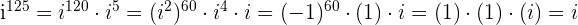
4
Números imaginarios puros
Un número imaginario puro se denota por:
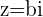
donde:
 es un número real.
es un número real.
 es la unidad imaginaria.
es la unidad imaginaria.
Recordemos que su parte real es  , es decir,
, es decir, 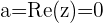 . A los números complejos cuya parte real es distinta de cero también se les puede llamar simplemente números imaginarios.
. A los números complejos cuya parte real es distinta de cero también se les puede llamar simplemente números imaginarios.
Operaciones de complejos en forma binómica
Suma y diferencia de números complejos
La regla para sumar o restar dos números complejos 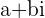 y
y  es sumar/restar parte real de uno con parte real del otro y parte imaginaria de uno con parte imaginaria del otro.
es sumar/restar parte real de uno con parte real del otro y parte imaginaria de uno con parte imaginaria del otro.
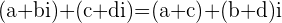

Cuando se tienen suma y resta combinadas de varios números complejos, se suman y/o restan las partes reales con las partes reales y las partes imaginarias con las partes imaginarias.
Ejemplos:
1
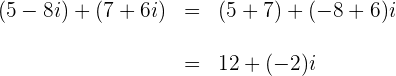
2

3
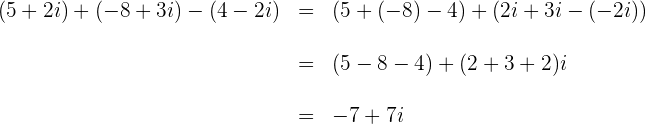
Ejemplo:

Producto de números complejos
El producto o multiplicación de números complejos expresados en la forma binómica se opera de acuerdo a la siguiente fórmula:
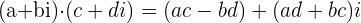
o también puede efectuarse como el producto de binomios.
Ejemplo de acuerdo a la fórmula:

Ejemplo como producto de binomios:
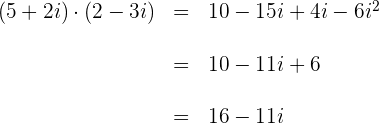
Cociente de números complejos
La división de dos números complejos expresados como fracción se efectúa multiplicando tanto el numerador como el denominador de dicha fracción por el complejo conjugado del denominador y, posteriormente, realizando las simplificaciones correspondientes hasta expresar el resultado de la forma  .
.
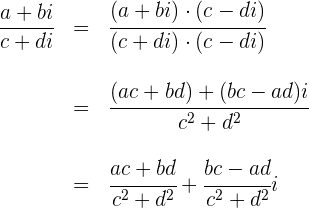
Ejemplos:
1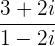
2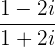
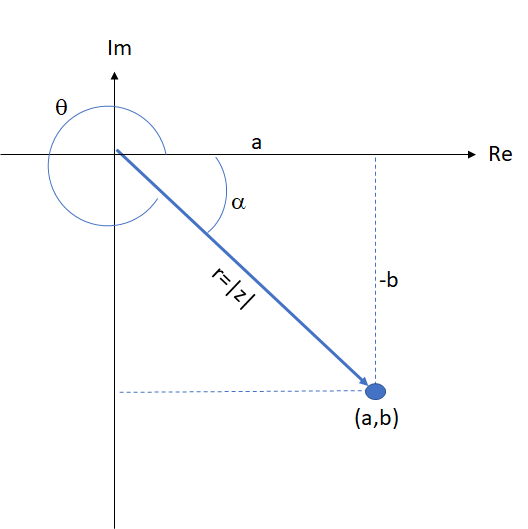
Modulo y argumento de números complejos
El módulo de un número complejo (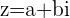 ) representado gráficamente es la medida del vector desde su punto inicial (origen) hasta su afijo o punto final
) representado gráficamente es la medida del vector desde su punto inicial (origen) hasta su afijo o punto final  Se designa por
Se designa por 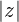 .
.
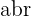 de la siguiente figura, se obtiene la fórmula para calcular el módulo de un número complejo:
de la siguiente figura, se obtiene la fórmula para calcular el módulo de un número complejo: 
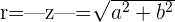
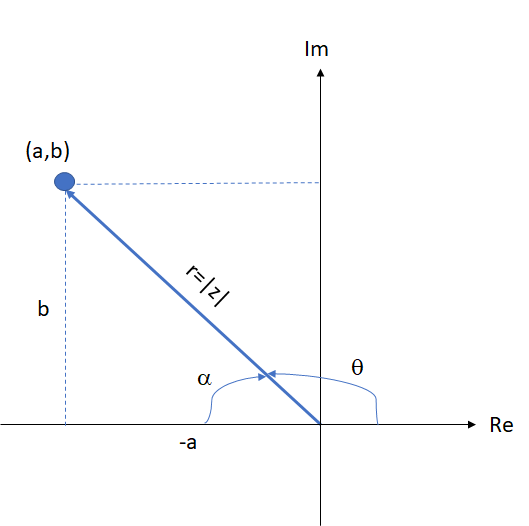
El argumento de un número complejo es el ángulo positivo ( el cual gira en sentido contrario a las manecillas del reloj) que forma el vector con la parte positiva del eje real. Se designa por 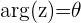 y se calcula mediante las siguientes fórmulas, dependiendo el cuadrante en el que se ubica el número complejo.
y se calcula mediante las siguientes fórmulas, dependiendo el cuadrante en el que se ubica el número complejo.
Primer cuadrante
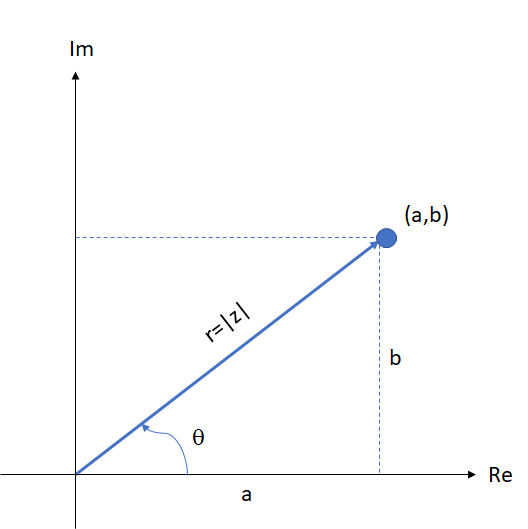

Segundo cuadrante

Tercer cuadrante

Cuarto cuadrante

Ejemplos: Calculemos el módulo y el argumento de los siguientes números complejos. También hagamos su representación gráfica.
1 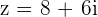
Calculamos el módulo

Calculamos el argumento
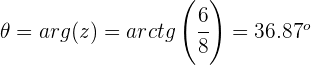
Representación gráfica

2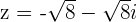
Calculamos el módulo
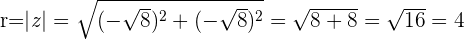
Calculamos el argumento
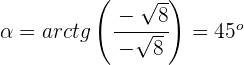
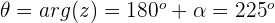
Representación gráfica

Números complejos en forma polar y trigonométrica
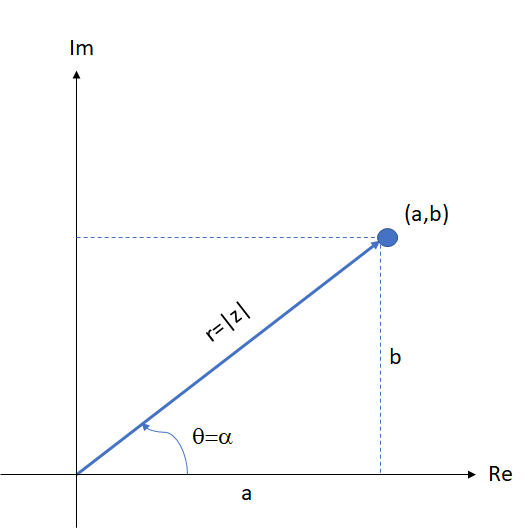
Para obtener las partes real e imaginaria  y
y  respectivamente, del número complejo en función de su modulo y de su argumento, se aplican las definiciones de las funciones seno y coseno al ángulo
respectivamente, del número complejo en función de su modulo y de su argumento, se aplican las definiciones de las funciones seno y coseno al ángulo  en el triángulo
en el triángulo 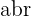 de la figura anterior.
de la figura anterior.

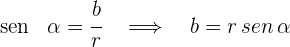
Posteriormente, la forma trigonométrica y polar del número completo se expresa así:

En la siguiente tabla se resumen las formas rectengular (binómica), polar y trigonométrica
de cualquier número complejo.
| Binómica | 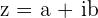 |
|---|---|
| Polar | 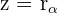 |
| Trigonométrica | 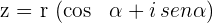 |
Números complejos iguales, conjugados y opuestos en las formas trigonométrica y polar
La siguiente gráfica muestra la representación tanto polar como trigonométrica de un número complejo 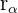 , su complejo conjugado
, su complejo conjugado 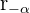 y su complejo opuesto
y su complejo opuesto 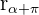 .
.

Números Complejos Iguales
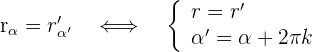

Números Complejos Conjugados


Números Complejos Opuestos


Producto de números complejos en forma polar
Fórmula

Ejemplos:
1

2

Producto por un número complejo de módulo 1
Al multiplicar un número complejo 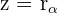 por
por  se gira
se gira  un ángulo
un ángulo  alrededor del origen.
alrededor del origen.
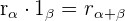
Cociente de números complejos en forma polar
Fórmula:

Ejemplos:
1

2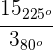
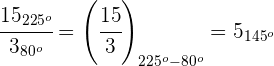
Potencia de números complejos en forma polar
Fórmula:

Ejemplos:
1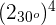
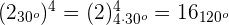
2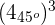

Fórmula de DeMoivre
El Teorema de DeMoivre sirve para obtener potenciaciones enteras positivas de números complejos expresados en su forma trigonométrica.
La fórmula de DeMoivre es:
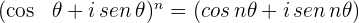
Si se aplica a la  -ésima potencia de un número complejo expresado en su forma polar:
-ésima potencia de un número complejo expresado en su forma polar:
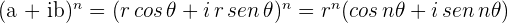
Ejemplo:
Se va a efectuar la potenciación del siguinte numero complejo expresado en su forma binómica, utilizado la forma trigonométrica y el teorema de DeMoivre, ya que empleando expansión binomial se haría algo tardado y tedioso.

Paso 1. Se calcula el modulo y el argumento de la base de la potenciación, que es el número complejo sin exponente.
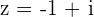
Módulo:

Argumento:
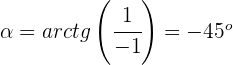
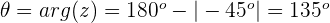
Paso 2. Se expresa el número complejo en su forma trigonométrica
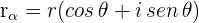

Paso 3. Se aplica la fórmula de DeMoivre.

Paso 4. Se escribe el resultado sin procedimiento.

Raíz n-ésima de números complejos en forma polar
Todo número complejo (excepto el cero) tiene exactamente  raíces n - ésimas diferentes.
raíces n - ésimas diferentes.


Ejemplo:

Paso 1. Se calculan el módulo y argumento del número complejo del cual se está extrayendo raíz sexta

Módulo
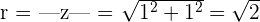
Argumento
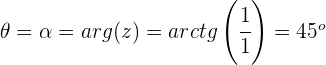
Paso 2. Se sustituyen los datos en la fórmula para extraer las 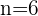 ráices n- ésimas del número complejo
ráices n- ésimas del número complejo  .
.

Paso 3. Se varía el valor de  desde
desde  hasta
hasta  para obtener las
para obtener las  raíces n-ésimas de
raíces n-ésimas de 
Para 
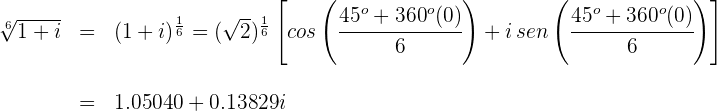
Para 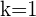

Para 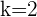

Para 
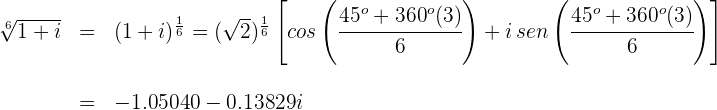
Para 
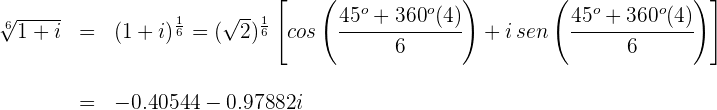
Para 
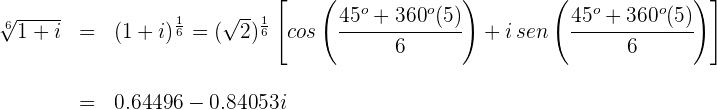
Representación gráfica de las  raíces del número complejo
raíces del número complejo 
Co-autor: Luis Felipe Velázquez León













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me podrá ayudar a resolver el siguiente número complejo encuentra su forma polar y la octava potencia Z= 3 + 2i
Hola. ¿Me podrían ayudar con el siguiente ejercicio de números complejos?: “si dividimos un numero complejo z= a + bi entre su conjugado, obtenemos su opuesto mas 1+2i. ¿de que numero z se trata?”
Raíz sexta de menos 625
Quiero pasar -4 + 2i a forma trigonométrica y con procedimiento
¿ cómo graficar P( -3, 60°, 30°) ?
podrian resolver este ejercicio paso a paso por favor!
(-√3 + i)⁸
Z= 59049 300° Hallar y Escribir en forma polar la quinta y la novena raíz de
10 Z
Es necesario hallar una por una las potencias para calcular i1000
Si te refieres a i elevado a la 1000, no.
Primero calculas i a las potencias 0,1,2 y 3, después el 100 lo divides entre 4 y lo que quede de residuo lo usas de potencia de i y ese es el resultado.
Sea el o los números complejos z = y ||z|| = √13, el o los valores de x es/son:
•5
•+-5
•12
•+-12