Temas
Se llama intervalo al conjunto de números reales comprendidos entre otros dos dados:  y
y  que se conocen como extremos del intervalo.
que se conocen como extremos del intervalo.
Intervalo abierto
Intervalo abierto  , es el conjunto de todos los números reales mayores que
, es el conjunto de todos los números reales mayores que  y menores que
y menores que  .
.
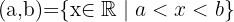
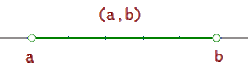
Intervalo cerrado
Intervalo cerrado  , es el conjunto de todos los números reales mayores o iguales que
, es el conjunto de todos los números reales mayores o iguales que  y menores o iguales que
y menores o iguales que  .
.
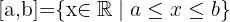
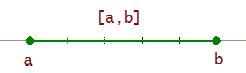
Intervalo semiabierto por la izquierda
Intervalo semiabierto por la izquierda  , es el conjunto de todos los números reales mayores que
, es el conjunto de todos los números reales mayores que  y menores o iguales que
y menores o iguales que  .
.

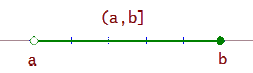
Intervalo semiabierto por la derecha
Intervalo semiabierto por la derecha  , es el conjunto de todos los números reales mayores o iguales que
, es el conjunto de todos los números reales mayores o iguales que  y menores que
y menores que  .
.
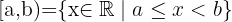
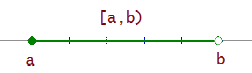
Semirrectas
x > a
Se define como el siguiente conjunto:
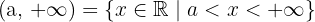

x ≥ a
Se define como el siguiente conjunto:
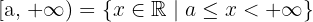

x < a
Se define como el siguiente conjunto:
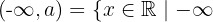

x ≤ a
Se define como el siguiente conjunto:
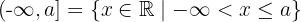

Cuando queremos nombrar un conjunto de puntos formado por dos o más de estos intervalos, se utiliza el signo 
Valor absoluto de un número real
El valor absoluto de un número real se define con la siguiente función:

Algunas propiedades del valor absolto
1
2 ·
·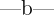
3 +
+ 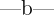
Distancia
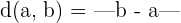
Entornos

 se expresa también
se expresa también  , o bien,
, o bien, 
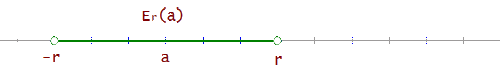
Entornos laterales
Por la izquierda
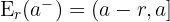
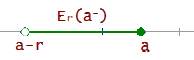
Por la derecha
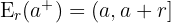
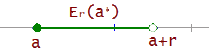
Entorno reducido

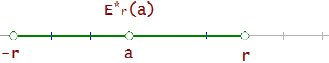














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cómo resuelvo la potencia de (5)2:(5)2=
7 1. -6 (3). (3):
Y (4/7)•(4/7)•(7/4)=
5. 4. 19
Y [3/8)]:(3/8)•3/8
Se puede tomar, a) x-2>=1 y b) x-2<=-1 se resuelve uno por uno que concuerda con lo mostrado. Valentina Zapata 8c gracias por su explicación profesor
porque surge una fraccion mixta del caso uno ejemplo 2 alguien me podria explicar
Me aparecen desigualdades en el ejemplo que mencionas y ninguna fracción.
Si sigues teniendo duda con el resultado con gusto te respondemos.
Si te refieres al ejercicio |x-2|>=1, el resultado es correcto el método puede no ser claro.
Se recomienda tomar por casos, a) x-2>=1 y b) x-2<=-1 se resuelve cada uno y el resultado concuerda con lo mostrado.